博文
《走近混沌》-25-生命游戏-1
 精选
精选
|||
第二十五章﹕生命游戏-1
前面我们介绍了自组织现象和孤子现象。此类现象出现的原因,都与外力无关,而只与系统自身内部各单元之间的相互作用,特别是非线性作用有关。由于这种内部作用,通过自身演化,使得系统群体表现出某种自动结合在一起、形成有序结构的集体行为。
除了物理学之外,科学界的各个领域,以及社会、人文、经济、网络、市场等方方面面,都观察到无序到有序的转化过程。其中,生命进化是大家熟知的例子。生命起源一直是个重大的不解之谜,至今仍然众说纷纭。生命之谜藏身于DNA分子的自我复制现象中,DNA的自我复制需要蛋白质的参与,而蛋白质产生又依赖于DNA携带的信息,这话听起来有点像通常人们开玩笑时所调侃的“先有蛋还是先有鸡”的悖论。事实上也是如此,这个鸡与蛋的基本问题可以说至今未解,因为它在本质上问的就是生命如何起源?
无论如何,生命起源与自我复制的机制有关,科学家们很早就认识到这点。生物学家们在实验室里研究分子如何自我复制的问题,而数学家及理论物理学家们则希望用某种数学模型,在计算机上来模拟产生自我复制的现象。早在上世纪50年代,大数学家冯·诺依曼为模拟生物细胞的自我复制而提出了‘自动细胞机’的概念。但当时并未受到学术界重视,直到1970年,随着计算机技术的普及,剑桥大学的约翰·何顿·康维设计了一个叫做《生命游戏》的电脑游戏之后,‘自动细胞机’这个课题才吸引了科学家们的注意。
一九七零年十月, 美国趣味数学大师马丁·加德纳通过《科学美国人》杂志的“数学游戏”专栏, 将康维的“生命”游戏介绍给学术界之外的广大读者,一时吸引了各行业一大批人的兴趣。
所谓生命游戏,事实上并不是通常意义上的”游戏”, 它没有游戏玩家各方之间的竞争, 也谈不上输赢,可以把它归类为“仿真游戏”。事实上,也是因为它模拟和显示的图象,看起来颇似生命的出生和繁衍过程而得名为“生命”。

图(25.1):生命游戏是二维的‘自动细胞机’
游戏在一个类似于围棋棋盘一样的,但格子更为密集、数目更多、可以无限延伸的二维网中进行。例如,设想如图(25.1a)的方格网。每个方格中都可放置一个生命细胞,每个生命细胞只有两种状态:“生”或“死”。在图(25.1a)的方格网中,我们用黑色的方格表示该细胞为“生”, 空格(白色)表示该细胞为“死” 。或者换句话说,方格网中的黑色部分表示的是某个时候某种‘生命’的分布图。生命游戏想要模拟的就是:随着时间的流逝,这个分布图将如何一代一代的变化?
这里又要用上我们在本系列文章中已经打过多次交道的‘迭代法’。在此我们不妨回忆一下曾经用过的迭代法:我们用迭代法画出了曼德勃罗集、朱利亚集等各种分形;用迭代法研究过逻辑斯蒂系统中的倍周期分岔现象,系统的稳定性、从有序到无序的过渡;还用迭代法求解洛伦茨方程及限制性三体问题的数值解。那么,这生命游戏用的迭代法有点什么不同呢?在画分形图和倍周期分岔图时,我们考虑的是系统的‘长期行为’,画出的是固定的,不随时间而变化的图形;画微分方程的数值解时,曲线是随时间而变化的函数,但是那只是空间中的一个点的轨迹。而在生命游戏中,考虑的是整个平面上的‘生命细胞’分布情况的演化过程。也就是说,平面上每个点的‘生死’状态都在不停地变化着。可想而知,这种迭代过程看起来将会生动有趣多了,否则,怎么会把它称之为‘游戏’呢。
游戏开始时, 每个细胞可以随机地(或给定地)被设定为“生”或“死”之一的某个状态, 然后,根据某种规则,计算出下一代每个细胞的状态,画出下一代的生死分布图。
应该规定什么样的迭代规则呢?我们需要一个简单的,但又反映生命之间(格子和格子之间)既协同、又竞争的生存定律。为简单起见,最基本的考虑是假设每一个细胞都遵循完全一样的生存定律;再进一步,我们把细胞之间的相互影响只限制在最靠近该细胞的8个邻居中,参考图(25.1b)。也就是说,每个细胞迭代后的状态由该细胞及周围八个细胞目前的状态所决定。作了这些限制后,仍然还有很多方法,来规定‘生存定律’的具体细节。
例如,在‘康维的生命游戏’中,规定了如下三条‘生存定律’,(被称为规则B3/S23):
1. 如果8个邻居细胞中,有3个细胞为生,则迭代后该细胞状态为生;
2. 如果8个邻居细胞中,有2个细胞为生,则迭代后该细胞的生死状态保持不变;
3. 在其它情况下,迭代后该细胞状态为死。
上面的三条生存定律,你当然可以任意改动,发明出不同的‘生命游戏’。但那几条规则,也不是游戏的发明者康维随便想当然定出来的,其中暗藏着周围环境对生存的影响在内。比如第一条,8个邻居中有3个是活的,不多不少,这种情况也许对中间的小生命是最理想的,因此,迭代后结果总是为‘生’;第二条,8个邻居中有2个是活的,人气不太旺盛哦,不过也还算马马虎虎吧,对中间的小生命影响不大,所以康维认为,生死可以维持原状;第三条就包括了好几种情况啦,一是8个邻居中活的数目多于4个,太挤啦,将造成物质缺乏,只有死路一条;或者是,8个邻居几乎全死光了,顶多只有一个奄奄一息的,那样的话,中间的小生命也难以生存,死定了。
如此定下了生存定律之后,对格子网的某种初始分布图,就可以决定每个格子下一代的状态,然后,同时更新所有的状态,得到第二代的分布图。这样一代一代地作下去,以至无穷。比如说,在图(25.2)中,从第一代开始,画出了四代细胞分布的变化情况。第一代时,图中有四个活细胞(黑色格子),然后,读者可以根据以上所述的四条生存定律,得到第二、三、四代的情况,观察并验证图(25.2)的结论。
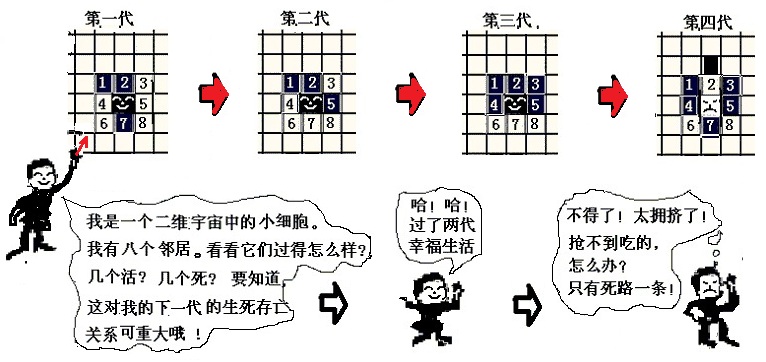
图(25.2):二维生命细胞的四代演化过程
你可能会说,这样的游戏玩起来真是太不方便了!一格一格地算半天才走一步,也看不出趣味在何处。不过,有了计算机的帮助,就不难发现生命游戏的趣味所在了。我们可以根据四条生存定律编好程序,输入初始状态图,用计算机很快地来进行一代一代的运算和显示。图(25.3)所演示的便是计算机的仿真结果,初始分布如图中n=0的小图所示,接下来,便是第5、7、30、50、100、150代之后的分布图。需要注意,图中计算机画出的图形颜色正好与我们刚才的规定相反:黑色背景部分表示没有‘生命’,其余的彩色部分(除黑色之外的任何颜色)则表示生命的分布情形。
(这个计算机生成的图中,黑色部分表示‘死’,其它彩色表示‘生’)
如果仔细观察图(25.3)所示生命游戏图形的演化过程,能发现几个有趣现象。看看最初始的分布图(n=0)中,可将‘活’的细胞分为左中右三群:左边一群不密不疏,最后的演化结果只剩下了一个固定的四边图形;中间的那一群非常分散,人烟过分稀少,第二代就全部死光了;最为有趣的是右边那一群,开始时人口密集,挤得够呛!因此第二代也死掉不少。但是后来,人口逐渐迁移分散,群体得到了更大的空间,从n=50之后,这群人口大幅度增长,子孙繁衍到各处。
https://blog.sciencenet.cn/blog-677221-631600.html
上一篇:《走近混沌》-24-孤立子的故事
下一篇:《走近混沌》-26-生命游戏-2
17 李伟钢 沈惠川 王春艳 陈国文 彭真明 温世正 鲍得海 董焱章 李泳 陆俊茜 苏力宏 JINDUI qianxun1991gmai zhanghuatian anran123 crossludo dameidebing
