博文
《走近混沌》-19-混沌魔鬼的诞生
 精选
精选
|||
第十九章﹕从有序到混沌
让我们仔细考察上一章中的图(18.2),复习一下罗伯特·梅的结论。从图中我们看到:可以将系统的长期行为大概归类于几种情况。或者说,可将图中的曲线分成特征不同的几个部分:
1. 当k小于1的时候,xn的最后极限是0,表明出生率太低,出生的数目补偿不了死亡数, 种族最终走向灭绝。例如,k=0.8,因为x0=0.1,不难算出x1=0.072,x2=0.051,……,对应的群体数分别是1000、720、510……,绝对群体数将逐年减少,最后趋于0。这种情况,连种族都灭亡了,显然也不存在什么混沌魔鬼。
2. 我们更感兴趣k大于1的情形,这时,方程中的第一项使得群体数逐年增长,而第二项使得群体数不能增长到无限大。我们将k值从1到3的那段绿线称为‘平衡’期,因为在这种情形下,生死速率旗鼓相当, 最后的群体数将平衡于一个固定值。比如,k=1.2,这时的线性增长率为120%。那么,许多年之后,这种生物会有多少呢?从x0开始,可以算出:x1=0.108,x2=0.1157,……。因而,相应的绝对群体数是1000,1080,1157,……。可以证明,若干年之后,这种生物的群体数将趋向于一个固定值:1666。所以,k值从1到3的情况下,种族数收敛到固定值,完全是经典情况,没有看见混沌魔鬼。
3. 当k=3.8,从迭代可以得到相应的绝对群体数是1000,3420,……,6547,9120,3100,8120,……。这时的最后结果很奇怪,不会收敛到任何稳定状态,而是在无穷多个不同的数值中无规则地跳来跳去。也就是说:魔鬼跳出来了,系统走向混沌。
上面的第一、二种情况,属于经典有序,第三种,则为混沌。因而,我们最感兴趣的是中间从k=3到k=3.8的一段,我们再将这段放大来研究,即可得到图(19.1)中上图所示的曲线。
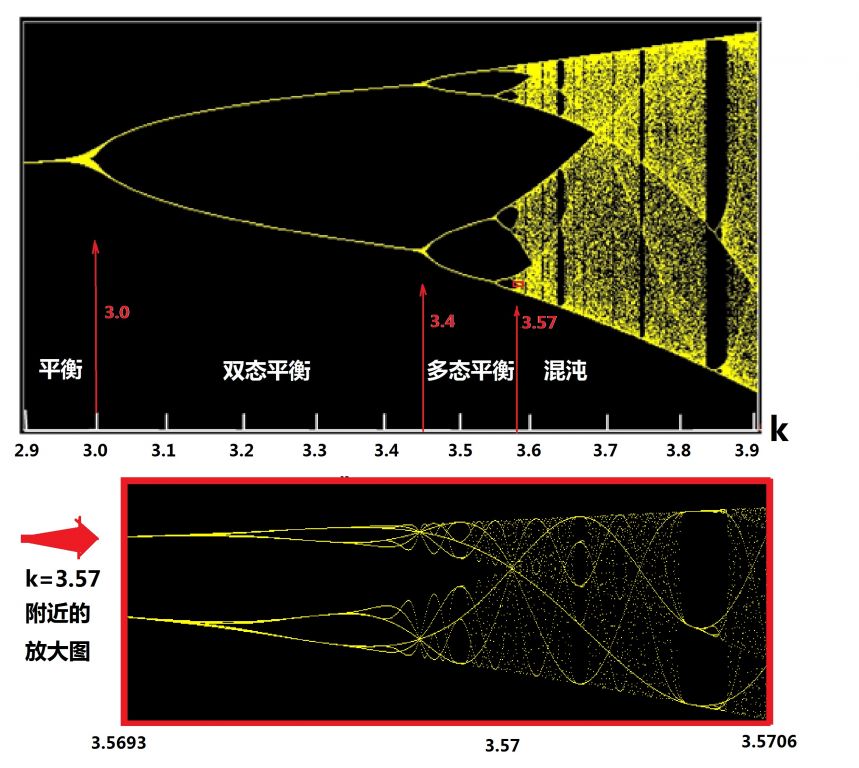
逻辑斯蒂系统是如何从有序过渡到混沌的呢?从图(19.1)的上图中可看到,即使我们让k的数值平滑地增长,系统的长期行为却不‘平滑’。当k的数值在3附近的时候,系统来了个‘突变’:原来的一条曲线分成了两支,形成一个三岔路口! 然后,k的数值继续平滑增长,到3.45附近时,又走到了三岔路口,两条曲线分成了四支,再后来,分成了八支,十六支……分支越来越多,相邻三岔路口间的距离却越来越短,最后,以至于我们的眼睛无法清楚地分辨那些三岔路口及分支为止。
现在,可能很多读者已经有了直觉:混沌魔鬼是由这些越来越多的分岔现象产生出来的!完全没错,这也是当时罗伯特·梅的结论。人们将这种分岔现象叫做‘倍周期分岔’现象(Bifurcation)。‘周期’这个词是哪儿冒出来的呢?想想我们所研究的逻辑斯蒂方程(18.3),这是个一代一代(或者说一年一年)的迭代方程,那么,一年就是一个周期。我们观察k=3到k=3.4之间的曲线,也就是在图(19.1)中标示为‘双态平衡’的那一段),所谓‘双态平衡’ 意味着,迭代到最后,每年的群体数将在两个数值之间循环。也可以说, 系统回到原来状态的周期从一年变成了两年,周期加倍了!后来,从k=3.4到k=3.57,状态数越来越多,最终的群体数将在更多的数值之间循环, 因此,系统回到某一平衡状态的周期因加倍又加倍而变得越来越长,这是图中标示为‘多态平衡’的一段。
当k增加到3.57之后, 由于分支之间的交互缠绕, 已无法区分单独的分支, 倍周期分岔现象呈崩溃之势, 平衡点已无法区分,连接成一片连续区域。这意味着最终的群体数失去了周期性, 进入图中标示为‘混沌’的范围。点击图(19.1),可链接到JAVA演示程序,用鼠标右键画个小矩形,便可将k=3.75附近区域放大,得到图(19.1)中下面的图形。
上面所描述的系统状态随着参数的变化从平衡走向混沌的过程, 不仅仅出现在生态学中,而是一个普遍现象。倍周期分岔现象是系统出现混沌的先兆,最终会导致有序到无序, 稳态向混沌的转变。我们在前面章节中介绍洛伦茨吸引子时,洛伦茨方程中也有一个参数,那是叫做瑞利数的R。瑞利数表征了大气流的粘滞性等物理特征。当时,洛伦茨在他的系统中所用的瑞利数R=28,得到了混沌现象。对某些其它的R值,有混沌解,也有非混沌解。因此,当R平滑变化时,在洛伦茨系统中,也能观察到倍周期分岔现象,从而观察到系统从有序过渡到混沌的过程。
科学家们更为深入地研究倍周期分岔图, 总结出倍周期分岔现象具有自相似性及普适性等等重要而有趣的特征。
自相似性是显而易见的。如果将图(19.1)中的倍周期分岔曲线在不同的标度下进行放大, 仔细观察, 就会发现它实际上是一种分形, 一种具有无穷嵌套的自相似结构, 或所谓标度不变性: 即用放大镜将细节部分放大若干倍后,它仍与整体具有相似的结构。这个与内在随机性密切相关的几何性质揭示了倍周期分岔现象与分形、混沌、奇异吸引子等之间的内在联系。
我们将在下一章继续讨论倍周期分岔现象的其他有趣特性。
https://blog.sciencenet.cn/blog-677221-620215.html
上一篇:《走近混沌》-18-生态繁衍和混沌
下一篇:《走近混沌》-20-混沌魔鬼‘不稳定’