博文
弱依赖多层网络上级联失效动力学
|
在一些复杂系统中,一个网络中某个节点的失效可能不会导致其他网络中依赖与他的节点完全失效,而是造成一定程度的损害。因此,弱依赖的多层网络更具有一般性。在弱依赖的情形下,多层网络的性质会与强依赖的情况有明显的不同。首先,网络与网络之间耦合拓扑结构会对网络的级联失效动力学有着强烈的影响。而对于强耦合的多层网络中的一组相依节点,一旦其中一个节点失效,其余节点也就完全失效,它们之间的依赖结构不会对系统有显著影响。正因为如此,对于弱依赖的多层网络,不同网络层的渗流阈值和渗流相变的类型也不相同。网络层的超级度越大,其渗流阈值就越大,鲁棒性也就越差。同时,一些超级度较大的网络层在渗流时可能表现为一阶不连续相变,而一些超级度较小的网络层的渗流相变类型为二阶连续相变,在超级度较大的网络发生渗流时,会导致其已经发生渗流的最近邻网络再次发生相变,从而导致系统中出现多重相变现象。
在强依赖的多层网络模型中,一个节点的失效会导致其依赖节点完全失效,这是一种点对点的强相互作用[1]。这一假设虽然能够刻画一些现实系统之间的节点耦合机制,如因特网中的节点对电力网络中节点的依赖。但是在存在缓冲或应急机制情况下,这一假设就会显得过于简单而直接,如一些基础设施的节点可能存在备用电源,当电网故障时,它可能会因电力供应的减少而维持部分主要功能。为了描述这种弱耦合机制,我们提出了一种点对边的相互作用机制。当一个节点失效的时候,其依赖节点的部分功能会受到损害而失去一些连接。具体而言,假如A网络中的一个节点Ai依赖于B网络的节点Bi,如果节点Ai失效,节点Bi的每一条边都有1-α的概率被删除(α的概率保留);反之亦然。当α=1的时候,网络之间的依赖性最弱,而当α=0的时候,网络的依赖性最强,此时等价于强依赖的多层网络。
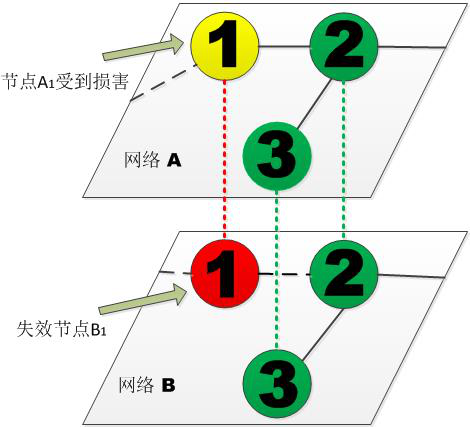
图1:节点弱耦合机制示意图。节点B1因受到攻击而失效,节点A1因与B1的依赖而受到损害,失去了一条边(段状直线)。
当某个网络层X中的一部分节点失效的时候,与这些失效节点有依赖性的节点就会受到损害而损失一些边,从而导致他们所在的网络发生破碎,只有属于这些破碎网络中巨分支的节点才能保持功能,而其它较小碎片中的节点就会失效。这些失效的节点又会导致其他网络层(包括X)中的相互依赖的节点受到损害,从而导致这些节点连接的删除而引起网络的破碎。在这种依赖失效和破碎失效的交替作用下,级联失效随之产生。当网络到达稳态的时候,我们用每个网络层中存活节点的比例来评估网络的鲁棒性。
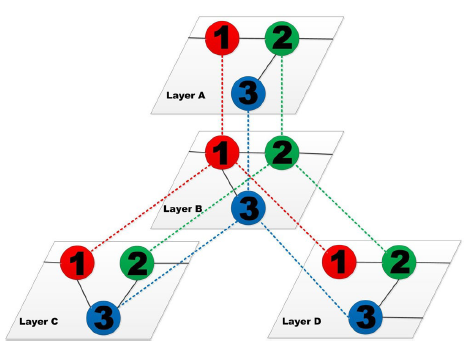
图2 星形多层网络示意图。网络层B为中心,ACD为周边网络层。
对于一个星型结构的四层网络,假定每一层的度分布完全相同记为P(k),如图2所示。给定平均度z,由于每一个网络都由一些分支组成,我们将那些不属于网路巨分支的节点视为失效节点。网络在经过一个“依赖失效-破碎失效”跌代过程后到达稳态,我们将关注不同网络层的巨分支随网络平均度z的变化情况。我们可以发现,对于α=0.9,0.8,0.7时,中心网络B最后发生渗流相变,而边缘网络最先发生渗流。当中心网络发生渗流的时候,边缘网络ACD会发生第二次相变,导致出现了多重相变的现象。而当α较小的时候,所有网络层同时发生渗流相变。这一结果说明,网络渗流阈值与其位置和超级度有很大的关系。同时我们发现,对于一些适度的α,周边网络渗流相变的类型为连续相变,而中心网络的渗流相变类型为不连续相变。这又说明网络渗流相变的类型也与网络的位置和超级度有关。
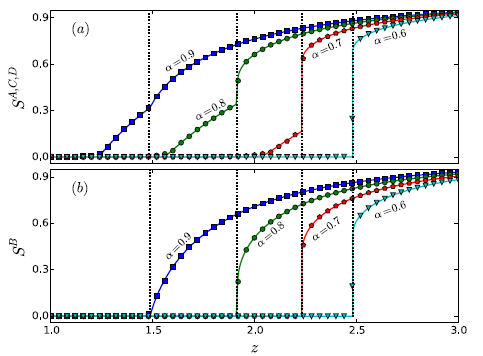
图3 星形多层网络渗流。
对于树形的多层网络,我们仍然可以发现类似的现象。这一模型的理论解析和更详细的结果可以查阅文献:https://www.nature.com/articles/s41598-018-20019-7
多层网络渗流和鲁棒性的研究仍然是目前的热门问题之一,弱依赖机制可以在更多多层网络模型中进行扩展,如考虑结构性质对多层网络对于网络鲁棒性的影响,如同配性[4],重叠边[5],空间嵌入[6]等,或弱依赖性对多层网络恢复[7],免疫[8]和强化[9]的作用等。此外基于弱依赖的特性,我们还可以考虑多层网络中节点依赖的非对称性[10],多样性[11]对网络的鲁棒性的作用。
参考文献:
[1] Buldyrev, S. V., Parshani, R., Paul, G., Stanley, H. E. & Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature(London) 464, 1025–1028 (2010).
[2] Gao, J., Buldyrev, S. V., Havlin, S. & Stanley, H. E. Robustness of a network of networks. Phys. Rev. Lett. 107, 195701 (2011).
[3] Gao, J., Buldyrev, S. V., Stanley, H. E. & Havlin, S. Networks formed from interdependent networks. Nat. Phys. 8, 40–48 (2012).
[4] D. Zhou, A. Bashan, R. Cohen, Y. Berezin, N. Shnerb, and S. Havlin, Simultaneous first-and second-order percolation transitions in interdependent networks, Phys. Rev. E 90, 012803 (2014).
[5] Y. Hu, D. Zhou, R. Zhang, Z. Han, C. Rozenblat, and S. Havlin, Percolation of interdependent networks with intersimilarity, Phys. Rev. E 88, 052805 (2013).
[6] A. Bashan, Y. Berezin, S. V. Buldyrev, and S. Havlin, The extreme vulnerability of interdependent spatially embedded networks, Nat. Phys. 9, 667–672 (2013).
[7] K. Gong, J.-J. Wu, Y. Liu, Q. Li, R.-R. Liu, and M. Tang,The effective healing strategy against localized attacks on interdependent spatially embedded networks, Complexity 2019,1–10 (2019).
[8] D. Zhao, L.Wang, S. Li, Z.Wang, L.Wang, and B. Gao, Immunization of epidemics in multiplex networks, PloS One , e112018 (2014).
[9] X. Yuan, Y. Hu, H. E. Stanley, and S. Havlin, Eradicating catastrophic collapse in interdependent networks via reinforced nodes, Proc. Nat. Acad. Sci. (USA) 114, 3311–3315 (2017).
[10] R.-R. Liu, C.-X. Jia, and Y.-C. Lai, Asymmetry in interdependence makes a multilayer system more robust against cascading failures, Phys. Rev. E 100, 052306 (2019).
[11] L.-W. Kong, M. Li, R.-R. Liu, and B.-H. Wang, Percolation on networks with weak and heterogeneous dependency, Phys. Rev. E 95, 032301(2017).
https://blog.sciencenet.cn/blog-627222-1229185.html
上一篇:随机网络中级联失效动力学:相变行为的交叉
下一篇:多层网络级联失效中的深度穿透和广度扩展