博文
神奇的超流
||
超流 Superfluid

神奇而又真实
超流体是一种物态,特点是完全失去粘性。如果将超流体放置于环状的容器中,由于没有摩擦力,它可以永无止尽地流动。它能以零阻力通过毛细管,甚至能从碗中向上“滴”出而逃逸。
液氦在2.17 K以下时,它的摩擦系数变为零,这时液态氦可以流过半径为十的负五次方厘米的小孔或毛细管,这种现象叫做超流现象(Superfluidity),这种液体叫做超流体(Superfluid)。

上图取自wiki
超流体是物质在没有能量损失的情况下无限流动的一种物相。这种特性是由 Pyotr Leonidovich Kapitsa, John F. Allen 和 Don Misener 在1937年发现的。至少有两种氦的同位素、一种铷的同位素和一种锂的同位素可以在极低温下实现。
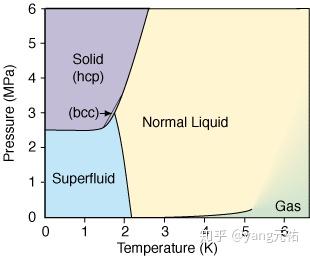
只有液体和气体才能是超流体。例如,氦的凝固点是1k(25个大气压),4He 的超流性质出现在 2k 左右。当体系中所有原子占据相同的量子态时,就会发生超流相变。当原子被放在非常近的位置,冷却到它们的量子波函数开始重叠,原子失去它们各自的特性时,就会发生这种情况,表现得更像一个超级原子,而不是一堆原子。
不寻常的行为都来自量子力学效应
发现
氦的稳定同位素是氦-3(或3He),有两个质子和一个中子;氦-4(或4He),有两个质子和两个中子。 4He 是大量天然存在的,自1950年以来,由于核反应堆中氚的衰变,已形成较轻的同位素3He。
这两种氦同位素在低压下都保持液态,直到绝对零度,并且都显示出超流特性,尽管在这两种情况下发生的温度非常不同。1937年, 苏联物理学家Pyotr Leonidovich Kapitsa, 和加拿大物理学家John F. Allen 和 Don Misener ,在低于2.17 K的温度下,在4He 中发现了超流态(无摩擦的形式流过狭窄毛细管)。(转变到超流体相被称为 lambda 相变。)轻同位素3He丝毫没有超流态的痕迹或任何其他异常行为。 但在1972年,美国物理学家Douglas D. Osheroff,Robert C. Richardson, and David M. Lee 发现低于2.65 K下, 3He 液体有三个不同的反常相,,称为 A, B, 和 A1,都显示许多相同的奇异现象, 虽然不像 4He 超流体那样引人注目。因此,这些相统称为 3He 超流体 。
超流相的行为
液体 4He 转变到超流相最引人注目的特征是,在微小的毛细管中突然出现没有摩擦地流动能力,任何普通的液体(包括4He本身在 λ 相变之上)都会被它的粘度卡住;因此,在所谓的正常相(即高于 λ 温度)下“氦气密封”的容器可能突然在其下方泄漏。在超流体相中观察到的相关现象包括在环形容器中维持持续流动的能力;液膜蠕变现象,液体在没有明显摩擦的情况下向上或越过装有液体的桶的一侧; 它的导热系数是正常相的几百万倍,比最好的金属导体的导热系数都大。另一个特性不那么壮观,但对于理解超流体相非常重要:如果液体在缓慢旋转的桶中冷却经 λ 相变,随着温度趋于绝对零度,即使桶继续旋转,液体也逐渐相对于实验室停止。这种非旋转效应是完全可逆的;旋转的表观速度仅取决于温度而不取决于系统的历史。大多数这类现象也在液体 3He 的超流体相中观察到,尽管形态稍差。
认为超流性与超导性之间存在着密切的联系;的确,从唯像学的观点来看,超导性就是发生在带电系统中的超流动性。因此,超流体 4He 通过狭窄毛细管的无摩擦流动与超导体中电子的无摩擦流动是平行的,而氦在环形容器中维持循环流动的能力与超导环中电流的持续存在非常相似。不那么明显的是,非旋转效应与超导体中的 Meissner 效应相似。在 4He 和 3He的超流体相中,还观察到了许多超导特性,如存在涡流以及约瑟夫森效应。
超流特性的理论解释
对于超流性(或超导性),公认的理论理解基于的观点是:大量的原子(或电子)表现出相同的,而且本质上是量子力学的行为;也就是说,这个系统是由一个单一的,相干的,量子力学波函数描述的。原子中的单个电子不能在任意轨道上绕原子核旋转;相反,量子力学要求角动量是量子化的。这也是原子抗磁性现象的起源。同样地,量子力学允许放置在环形容器中的单个原子(或分子)以一定的速度绕着环形运动。在像水这样的普通液体中,热无序确保原子(或分子)分布在不同的量子态上,这样平均速度就不会被量子化;因此,当容器旋转时,液体有足够的时间达到平衡,它就会按照日常经验随容器一起旋转。
在超流体系统中情况完全不同。更简单的例子是4He,这是一种由原子组成的液体,原子的自旋角动量为0,其可能状态之间的分布遵从玻色统计。这种原子之间没有相互作用的气体,在一定温度下,会发生一种称为玻色凝聚的现象;在 T0 温度以下,所有原子的有限部分处于一种状态,通常是能量最低的状态,当温度降至绝对零度时,这种状态会向一种状态叠加。这些原子是冷凝的。人们普遍认为,类似的现象也会发生在像 4He 这样的液体中,在这种液体中,原子间的相互作用是非常重要的,而 4He 的 λ 相变仅仅是 Bose 凝聚的开始。(这种现象在其它自旋为零的原子体系(如氖-22)中并不存在,原因很简单:随着温度的降低,首先发生的就是冻结。)如果是这样,那么,对于处于 λ 相变之下的温度,所有原子的有限部分必须合作决定它们都将处于哪个可能的量子态。特别是,如果容器以足够慢的速度旋转,这些凝聚原子将占据非旋转态,即,相对于实验室而言,它们将处于静止状态——而其余的将正常运行,并以随容器旋转的方式平均分布。因此,随着温度的降低和凝聚原子比例的增加,液体就会相对于实验室(或者更准确地说,相对于固定的恒星)逐渐趋于静止。同样,当液体流过一根细小的毛细管时,凝聚的原子不能被壁面散射,因为它们被玻色统计强制处于相同的状态。它们必须同时被分散。由于这一过程极不可能发生,所以液体,或者更准确地说,它的凝聚部分,流动没有任何明显的摩擦。超流性的其它特征表现可以用类似的方式来解释。
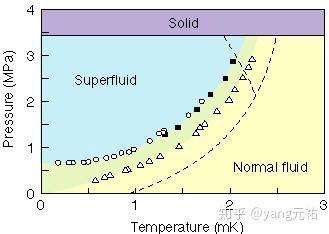
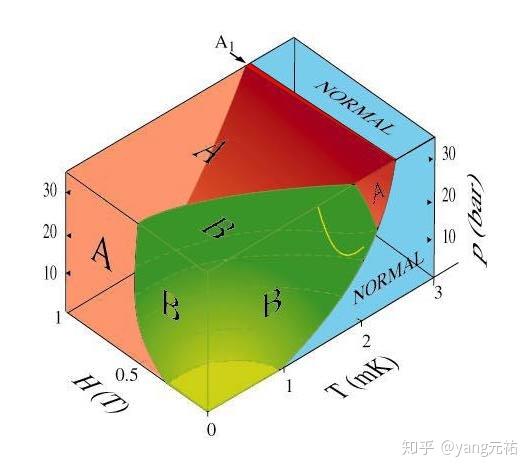
Phase Diagram of 3He in Aerogel
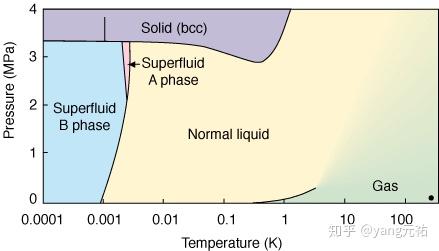
玻色凝聚的想法不能直接用于液体 3He ,因为 3He 的原子自旋角动量等于1/2(h / 2π的单位),因此它们的分布被认为是由另一个不同的原则所控制,被称为费米统计。然而,在 3He 的超流相,原子就像超导体中的电子一样,形成成对的库珀对——一种准分子络合物——具有整数自旋,因此有效地服从玻色而不是费米统计。特别是,一旦库珀对形成,它们就会经历一种玻色冷凝,然后上面提到的关于 4He 的论点他同样适用于它们。
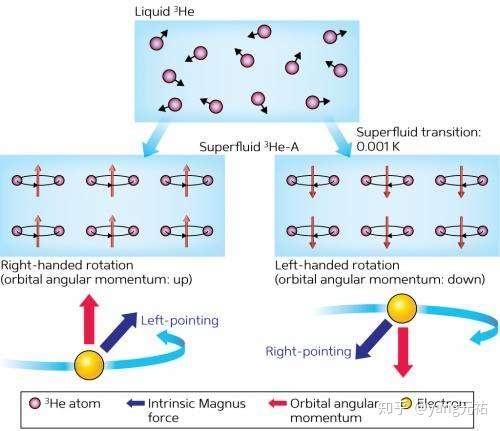
与超导体中的电子一样,有限的能量,即所谓的能隙Δ,对于破坏对(或至少大部分)是必要的,因此超流体 3He 的热力学与超导体非常相似。这两种情况之间存在一个重要区别。而在经典的超导体中,电子与相反自旋的电子配对并且具有零的总角动量,使得 Cooper 对的内部结构毫无特征,而在 3He 中,具有平行自旋和非零总角动量的原子对,使得内部结构更丰富,更有趣。这种情况的一个表现是存在三种液体 3He 的超流相,称为 A,B 和 A1,其区别在于 Cooper 对的不同内部结构。 B 相在大多数方面类似于传统的超导体,而 A(和 A1)相在其性质上具有强烈的各向异性,并且具有实际上在某些运动方向上消失的能隙。结果,A 和 A1 相的一些超流体性质明显不同于 4He 或 3He-B 相,并且在已知的物理系统中确实是独特的。
超流,超级溜
https://blog.sciencenet.cn/blog-566204-1157967.html
上一篇:薛定谔的猫
下一篇:科学网博客编辑器太老了,体验很差
