博文
摄影测量与计算机视觉(5) 上知天文、下知地理 下
 精选
精选
|||
摄影测量与计算机视觉
(5)上知天文、下知地理 下
1. 长风几万里?
明月出天山,苍茫云海间;长风几万里,吹度玉门关……。李白《关山月》,意境深远。“吹度玉门关”一句,应该是受了王之涣《出塞》(春风不度玉门关)的影响。既如此,我们不妨推测:这个风是从皇帝(长安)那吹过去的,经过X万里,到达玉门关(今敦煌)。X是多少?作为现代人,打开google地球。输入西安和敦煌,得到一条算比较直的路线:1719公里,合唐朝的3784里。唐朝三百步为一里,(李世民的)左右脚各迈一次为一步,一里约合今天的454米。要是从边境,浙江沿海吹起,合7700里。故最好的选择也只能填“一”了!现在我们的疑问是:唐朝的太史局和民众,是否对自己的疆土距离和面积一清二楚?我们来看看由僧一行领衔的一次空前的天文大地测量。
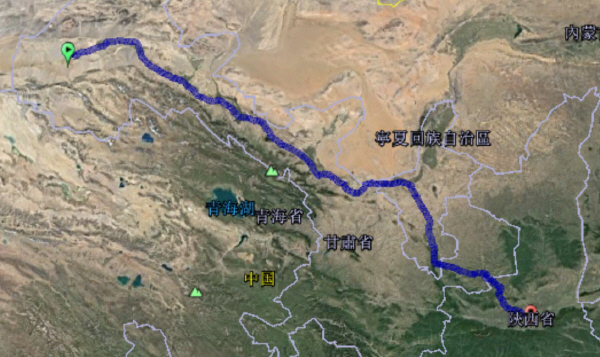
图1 轻轻一点。两地距离就知道了。古人怎么办呢?
一行俗名张遂,自幼聪明好学,当时誉为上知天文、下知地理、呼风唤雨、甚至无所不能。有过目不忘的本事。传说只看了一遍宫女名册(没有三千,也有数百),对姓名、年龄、职责等倒背如流,唐玄宗也对其低头行礼,口称圣人。少时读扬雄《太玄经》,数日贯通。太白诗云“谁能书阁下,白首太玄经”(出自太白《侠客行》,金庸也写过同名武侠)。可谓皓首穷经,难度可见一斑。更神奇的传说是:一行对围棋一窍不通,看了当时第一围棋高手王积薪下了一盘,就会了;马上与积薪对弈,居然不分胜负!相比之下,AlphaGo在学习了数十亿盘后,才打败李世石,可算天壤之别(小样本学习、无监督学习,也是深度学习当前最大的障碍、挑战和目标)。一行二十一岁出家,遍历天下。酷爱天文、地理和数学,听说浙江天台山的和尚精通数学,不远三千里,前去请教。在本职工作中(当和尚),也成为佛教密宗一代宗师。二十九岁时,受不住唐王朝屡屡邀请,勉强出山并从事天文历法和测量工作。为修正历法,进行了一场史无前例的全国性天文大地测量。
在他的主持下,全国布设了12个观察站,测量两分两至的日影,历时九年。最终测出纬度相差一度的子午线长,为世界首次。编制《大衍历》,提出“张遂内插公式”(早于欧洲900余年),制作了正切函数表(早于西方200多年)。《大衍历》沿用800余年至明末,并流传至日本、印度。他还根据历代星图,发现恒星也会改变位置,恒星不恒。比英国哈雷的发现要早900多年。发明“黄道游仪”(为什么黄道要动?上篇我们谈到,从晋代就发现了“岁差”,黄道的移动正是拟合岁差的需要),和“水运浑天仪”(不但演示日月星辰的视运动,也是世界上最早的自鸣钟)。这两个成就都超越了张衡。这里补充一下时刻的授时,其实比历法要简单。因为只要定了每日12时,经过线性均匀内插即可。唐代将一天分为100刻(每刻约14分钟),水运浑天仪每刻击鼓,每时辰撞钟。而历法,却受到日月视运动缓急的影响,因此才需要二次和三次非均匀内插法。当然,并不是说当时的二次、三次内插就是解高次方程,内插法仍是线性的。用现代的数学语言来说:
y = a + bt + ct2+ dt3(1)
其中,t,y是观测值,a,b,c,d才是真正的未知数。借助4组观测,解出未知数后,再由t(任意时刻)内插出对应的y(位置)。
一行虽然得到了1°子午线的长度,但他并未由此发现地球是圆的。笔者查了许多资料,也没有发现他用日影长度来反推两地距离,即唐王朝疆域的南北距离。我们只能猜测当时的疆域是分道测量所得(唐朝的地域行政单位称为“道”),所用的仪器是绳子。因此在山区和丘陵,以及州、道的交界处,误差是非常大的。由于唐朝以前的所有古地图都已遗失,我们这里放一幅明代的广舆图。广舆图是明清时代最重要的地图集,是中国制图的代表。但事实上广舆图是相当不精确的,方向只有八个,距离仅按道路。我们据此推断,在唐朝,人们对疆土的长度和面积是非常模糊的。

图2 明代广舆图
2. 高次方程,从花拉子密到牛顿
如果令式(1)中y=0,t为未知数,那就变成了一元三次方程。有文献表明,早在公元前480年,中国会解一些二次方程,但不知道通解;唐朝的数学家也给出了一些三次方程解的特例。公元11世纪,波斯的花拉子密(780-850)系统解决了二次方程解的问题。他被称作是“代数的创造者”,Algorithm正是他名字的拉丁文译名。当时阿拉伯的代数世界领先,深刻影响了西方的数学研究,十进制也是由花拉子密传到西方。花拉子密同张衡、一行一样,也是天文、地理研究的集大成者,甚至走得更远。他著有《信德及印度天文表》,包含日月五星的运行路径,以及类似一行创造的正弦表。他制造的日晷能够在世界各地使用(日晷是一种授时装置。除了上文所说的借匀速水力将24时等分外,日晷是古代常用的借助日影的授时装置。日光下,晷针在刻度盘上的投影,可读出时刻。晷针与水平面的夹角必须等于当地纬度才能精确授时。至于沙漏、燃香等更简单的方法我们就省略了)。在地理学上,花刺子密写了一本书,我们看名字就知道大致内容:《地球的地貌-城市、山岳、海洋、岛屿及河流,阿布·贾法尔·穆罕默德·伊本·穆萨·花拉子密据托密勒的地理作品所著》。
三次方程的通解发现者,属于700年后文艺复兴时期意大利的卡尔达诺和塔塔利亚。而四次方程的通解,是卡尔达诺的学生,意大利数学家费拉里(1522-1565)发现的。同时掌握三次方程和四次方程解的费拉里在一次辩论中轻松击败了塔塔利亚,导致后者在三次方程通解发现权的争夺中处于下风。
关于五次及以上高次方程通解,300年后由法国的数学家伽罗瓦(1811-1832)证明不存在。伽罗瓦英年早逝,令人惋惜;证明所用的工具,即他和同样英年早逝的数学家贝尔共创的群论,已经成为现代数学必不可少的部分。希望这能安慰他们的在天之灵吧。
高阶方程的通解缺失,并不意味着解不存在。在坐标系中画出诸如(1)的曲线,与x(t)轴只要相交,交点就是解。既然无法直捣黄龙,就需采用迂回战术。这就引出了另一个大人物:牛顿(1643 -1727)。牛顿发明的微积分,是现代科学——无论基础物理还是金融保险——的基石,如何称赞都不过分;牛顿也因此被称为最伟大的数学家之一。微积分的一个简单应用就是迂回求解高次方程(也可以解其他非线性方程),这种方法称为牛顿迭代法。摄影测量和计算机视觉中的几何解算部分,依赖于两个数学基础,一个就是迭代法(另一个是最小二乘,我们下个小节介绍)。既然如此,我们稍作展开。
依然从(1)出发,这里我们令a=2,b=3,c=12,d=3,我们得到了图3这样的一条曲线,求其与x轴的交点,即y=0是我们的目标。首先要明确,任何依赖迭代的法则,必须先有一个初值(在各个学科中名字有些区别:零点、初始条件、初始状态等,但本质相同)。这个初值以猜测为主,但也有一些猜的规则。比如说,这里我们可以令b=c=0,只保留最重要的高次项。然后得到三个解。取其中之一x0≈ -1.2为初值。此时y ≈ 18。现在,我们自然希望y值持续减小,直到0。如何减小?一种直观的、也是牛顿采取的方法,就是沿着当前的切线方向下降。曲线的切线怎么求?既然微分已经发明,我们直接求曲线在x0处的一阶导数y0’ = tgκ。然后,计算切线与x轴的交点x1。这时,根据切线的定义得到:tgκ = y0/(x0 – x1),稍作变形,即:
x1 = x0 – y0/ y0’ (2)
我们就得到了一次迭代的方程。同理,过x1作曲线的切线,交x轴于x2;如果继续过x2作切线交x轴于x3,你会发现x3处的y已经非常接近0了。那么牛顿迭代法的一般公式就是:
xn+1 = xn – yn/ yn’ (3)
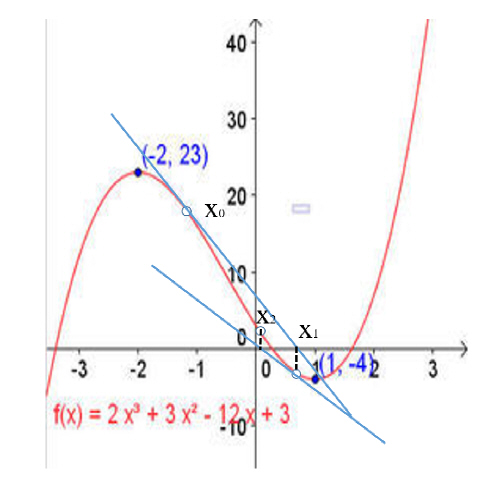
图3 牛顿迭代法。切线的舞蹈。
牛顿迭代法并非第一个求解高次方程的数值方法。在此之前,我国宋朝的数学家秦九韶在《数书九章》也提出高次方程的数值解法。没有微分作为基础,即无法求曲线的切线,因此他推导出一组更近似的迭代方法。首先将高次项写为:
f(x) = (((anx + an-1)x + an-2)x + ……+ a1)x + a0 (4)
迭代原则是:
f1 = anx+ an-1; f2 = f1x + an-2……; fn= fn-1x + a0 (5)
fn即解。秦九韶的方法由于n次必须迭代完成,所以大多数情况下,精度要比牛顿法低。当然牛顿迭代法也存在问题:(3)中分母上的导数不能为0,在导数很小时,可能超出收敛区域(收敛区域主要由x0决定,合适的x0,会保证迭代的正确收敛;而不恰当的初值,则会导致迭代发散或收敛于局部最小);在导数非常大时,每次迭代的增量很小,又导致收敛缓慢。针对这些情形,我们后续章节将介绍高斯法、共轭梯度法、LM等改进方法。
让我们再次回到式(1)。现在考虑a,b,c,d是未知数,而观测值,t和y却不止四组,这在测量中是非常普遍的。如何求解这样一个超定的线性方程组呢?高斯给出了一种经典方法——最小二乘。
3. 大地测量学家高斯
高斯(1777-1855)是最伟大的数学家之一,但毫无疑问,他是最伟大的大地测量学家,没有之一。他解决了两个问题:如何对大量的观测数据进行处理;如何用平面地图来展现地球椭球。前者导致的测量平差理论至今仍在使用;后者仍然是当前地图制作的标准,同时也为微分几何奠定了基础。
高斯生来就是神童。从1到100的连加算法妇孺皆知。18岁时,高斯刚刚进入哥廷根大学,就发明了最小二乘法。19岁时完成了正17边形的尺规作图。从1818年开始,高斯主导了汉诺威公国的大地测量工作,一直到1826年。事实上,后继的计算工作直到1848年才结束,历时30年!因此称他为大地测量学家名副其实。
我们这里先介绍高斯发明的最小二乘,地图投影后续章节再讨论。最小二乘是寻找一组参数,使得所有方程的误差平方和最小。二乘,即平方。对于式(1)而言,由于参数要满足的方程超过4个,无法保证每个方程都精确成立,设其误差为v,并将y挪到方程右边,替换为更通用的L,则
vi = a+ bti + cti2 + dti3 - Li(6a)
V = Ax – L (6b)
下标i代表方程组中的第i个;6b是6a的矩阵形式。最小二乘的目标是:∑vi2=min,或者||V||2 = min。||V||2自然是凸函数,其极值min出现在导数为0的位置。即:2VT’V = 0。将6b求导后代入,得到:
ATAx =-ATL (7a)
x = -(ATA)-1ATL(7b)
简单地说,高斯最小二乘就是在平方和最小的意义下,将超定方程组最终转化成了未知数与方程个数等价的方阵。
整个大地测量和摄影测量竟然建立在如此简单的式(6)和式(7)基础上,令人感叹。但转念一想,已然释怀。事实上,牛顿力学、量子力学,不也是线性方程(组)吗!广义相对论确实是高度非线性的,因而只有区区几个解。我们对非线性方程(包括非线性微分方程)的研究,依然任重道远。回过头来,对于测量中的非线性方程,我们就需要将最小二乘(式6,7)与牛顿迭代法(式2,3)结合,称为非线性最小二乘法。对于观测值中的粗差(outliers,gross errors),亦需要发展新的抗差算法。后续章节再容详述。
即使伟大如高斯,也要花30年才完成汉诺威公国(面积远小于我国的一个省)的测量,令人感喟万千。不过,新时代正悄悄降临。人类将第一次像鸟儿一样真正起飞。会当凌绝顶、一览众山小!
4. 飞艇和摄影测量的诞生
飞翔是人类几千年来的梦想。希腊神话中,代达罗斯为儿子伊卡洛斯制造了用蜡黏合的羽翼,并告诫他不能飞太高。由于飞翔而过于兴奋的伊卡洛斯忘了父亲的劝告,越飞越高,太阳将蜡融化,不幸摔死。真人版传说与此类似:不列颠李尔王的父亲,布拉达国王是人类史上第一次尝试飞翔的人,身披羽翼从城墙上一跃而下,也不幸摔死。
在空气动力学成熟之前,借助羽翼的飞翔纯属痴心妄想。那么,在莱特兄弟之前就不能飞起来吗?NO。
最直观的方法是寻找比空气更轻的东西。我们最熟悉的那个“上知天文、下知地理、呼风唤雨、甚至有逆天改命之能”的大人物,诸葛亮(181-234),曾经制造过“孔明灯”。这是所有热气球的始祖。相传当时诸葛亮受困平阳,四周重重围堵,亮放出孔明灯,从空中发出求救信号以脱险。热气球的原理大致如此:气球上部封闭,下部开小口。点燃烛火,球内空气变热变轻,压强减小,在外面冷空气的浮力作用下,得以升空。
一直到了18世纪,西方的孟格菲兄弟才重新发明热气球,并于1783年第一次载人航行。这算是人类最早的飞行记录了。除了热空气,另外一个比空气更轻之物,就是氢气了(或氦气等)。虽然氢气占宇宙所有可见物质的70%以上,但是在地球上得到纯氢可没那么容易。大规模生产要依赖电解水或者天然气的蒸汽重整。1874年,法国的罗伯特兄弟最先乘坐氢气球飞上天空。(看来人类飞行家先驱都是兄弟上阵。)人类对飞行是如此渴望,整整下个世纪(19世纪),可算是气球和飞艇的世纪。
(至于比空气更轻的东西,容我讲一个亲历的小故事。十二三岁的时候,一个漆黑的深夜。从梦中醒来,发现屋里漂浮着四个磷火(俗称鬼火),不胜惊讶。当时立刻想起课本上刚学过的“白磷40°自燃”,现在大概才二十七八度,这不可能!更奇怪的是磷火的形状。其中一个像倒悬的水滴,最正常的家伙;一个像哑铃,两头圆,中间一根细线相连;一个弯弯的,像猫的肋骨。应该还有一个,但形状不够奇特,没记住。暗蓝色的磷火静静漂浮在仿佛永恒的夜空。憋得难受,聚集所有勇气打开灯,上完厕所后,熄了灯。磷火受气流影响,果然移动了位置。从那时,偶尔想起此事,就去查查资料,但对磷火的研究实在太少。国内只能偶见新闻八卦,学术界根本没有;国外尚有几篇,但非对症。此疑问留待将来。)
乐极生悲,气球和飞艇在经过1个多世纪的狂欢后,飞艇时代谢幕,逐渐退出历史舞台。能耗更高的飞机倒成了飞行器的主流。试想,如果没有齐柏林飞艇——兴登堡号的一声巨响,窗外可能是浪漫的、五颜六色的、漫天飞艇的21世纪?
最早的用于测绘的像片,也是摄影于德国的飞艇。从那时起,航空摄影测量诞生,并逐渐从大地测量中分离出来,成为独立的分支。借助飞行器,以及一些双目视觉的知识(见第三篇),我们就可以从航摄像片中重新获取地物的距离、形状、大小、高程,并制作高度精确和真实的地图。要是飞的足够高,只要几十张像片就能覆盖汉诺威公国。把大地测量中数百万观测值的处理,压缩为百十个参数;把三十年变成一小时;把高斯(如果还活着)以及我们从繁琐的解算中解放出来。
时代继续进步。现在,我们有了全球导航系统(GPS,北斗,伽利略),有了高分辨率的成像卫星(Ikonos,Geo-eye,中国ZY系列等)和google地球,有了智能手机、导航地图和GIS。古代,最伟大的学者才能称作上知天文、下知地理;而今天,任何一个普通人也能感天知地。今人胜古人。而科学,就是最闪耀的指路明灯。
https://blog.sciencenet.cn/blog-520501-988745.html
上一篇:摄影测量与计算机视觉——(4)上知天文、下知地理 上
下一篇:摄影测量与计算机视觉 (6)几何变换的层次 上
10 黄永义 徐令予 王林平 杨正瓴 迟延崑 shenlu xiyouxiyou guhanxian zjzhaokeqin icgwang