博文
早期视觉中的图像处理 上
 精选
精选
|||
摄影测量与计算机视觉(8)
早期视觉中的图像处理 上
1. 金箍棒与无穷
“悟空,你可知道金箍棒中蕴藏着一个巨大的秘密?”“秘密?那是什么,菩萨?”“小至芥弥,大至无形。关于脉冲的秘密。”“什么是脉冲?”。
无穷的悖论,自古有之。西方最有名的是芝诺版“龟兔赛跑”。芝诺断言:只要乌龟先出发,兔子永远追不上。他的理由简单概括为:兔子移动了无穷小距离的同时,乌龟也移动了无穷小的距离。这是一个无穷小的比较问题。在不能定量地描述无穷小也分大小之前,该悖论确实难以反驳。微积分创立后,我们知道距离对无穷小时间的微分就是速度。速度是可以比较的,虽然瞬时移动量为无穷小,但通过对速度的积分,就能清晰地反驳悖论。当然,在某些意义上关于芝诺悖论的争议仍在持续。
在中国,著名的无穷悖论的例子是庄子的“一尺之棰,日取其半,万世不竭”。在数学上,这句话没错。因为1/2n在n取任意大数时,总能大于0。庄子只是说“万世”,而非无穷。在物理上,可就不成立了。现代物理表明,原子由夸克组成,夸克是物体的最基本单位。为何夸克无法细分?回顾卢瑟福散射实验。当时卢瑟福为验证原子中究竟是空无一物还是存在更基本的单元,用大量的α粒子击打仅有几个原子厚度的金箔。绝大多数粒子毫无阻拦地穿过,而少量粒子却打在金原子核上被弹射,从而确定了原子核的存在。同理,实验物理学家也可用粒子去击打夸克,结果是:什么也没有。对于“没有”的东西目前还谈不上再细分。
回到数学,绝大多数数学的应用(当然包括我们要谈的图像处理),包括数学本身,都离不开最基本的概念:函数;但碰到无穷的情形,也要好好思考一下是否符合函数的定义。悟空的金箍棒,小可藏在耳朵里,大可顶天立地。我们给个限制条件,就是金箍棒的体积恒定为1。那么,如果棒子不断变长,他就会越来越细。直到成为一条线,而高度则是无穷。将它放在1维数轴的零点上,得到:
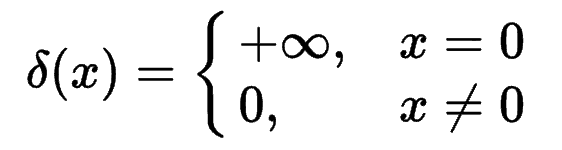
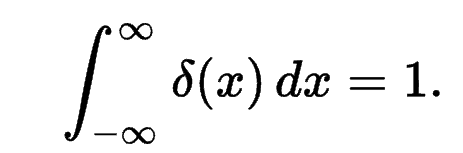 (1)
(1)
y=δ(x)显然不符合函数的定义,因为它的值域没有定义(无穷并不在实数R内),在定义域也不连续。如何描述悟空的金箍棒,困扰了数学家很多年,对“金箍棒”的逐渐深入的认识,也开辟了许多新的研究空间。其中之一,就是从“函数”发展为“分布或广义函数”。工科生在学习概率论时,可能迷惑于概率分布与函数之间的关系。确实,到这些概念的完全厘清,花了数学家几百年的时间。至于概率论自身也常常被诟病,直到上世纪的数学大师柯尔莫哥洛夫将其坚实地建立在测度论之上,争论才告平息。柯尔莫哥洛夫一生都献给了数学事业,硕果累累,桃李天下,是二十世纪最伟大的数学家之一。
简单地说:广义函数就是为了处理“金箍棒”这种不连续、极限条件下的特殊函数。其中广泛应用的一种广义函数称为“分布”。分布是什么?其实仍起源于牛顿和莱布尼兹的微积分。微分操作,要求函数“处处光滑可导”,条件何其苛刻?而积分则不然,虽然金箍棒兼备“不连续、无穷”这两大缺点,却仍然是可积的。可积分函数比可微函数要多得多。给定一个“函数”g,定义积分
∫g(x) φ(x)dx (2)
为g的分布。注意积分运算是线性的,分布其实是一个线性泛函。这里φ表示一个任意的“测试函数”,通常是紧致光滑且任意可导的函数。这里,我们并非直接研究g的性质,而是通过与测试函数的积分来间接观察它,换句话说,g将如何影响这个积分?具体地,金箍棒对应怎样的分布呢?这个分布又能起到什么作用?
2. 狄拉克δ函数
保罗*狄拉克是20世纪著名的物理学家,诺贝尔奖得主,量子力学的奠基人之一。在世人眼中,他聪明、淡泊,安静得过分。一位同事曾经开玩笑说:保罗说话可以当作时间单位,每说一个字,就是过了一个小时。狄拉克在推导量子力学公式的时候,无意中发现了金箍棒(现在叫做狄拉克函数)。
一个经典粒子可以用欧式空间中的位置和动量表达;那么:一个粒子的量子态如何表达?狄拉克创造了符号|a>以表示粒子的量子态,这是一个矢量;并在内积空间中将其展开:|a> = a1|x1> + a2|x2>+ a3|x3>… = ∑ai|xi>。基量子态|xi>相互正交,系数ai是标量,可看作每个基量子态相应的概率。将离散的求和写成连续的积分形式:
|a> = ∫f(x)|x>dx (3)
那么f(x)就是粒子在位置x处出现的概率,可写作<x|a>,它的物理意义为:在量子态|a>中找到量子态<x|的概率;在数学上实际上是内积运算<,>,即a在x上的投影。根据内积的定义,
f(x0) = < x0|a>= ∫f(x) < x0|x>dx (4)
对于任意一个x0成立。不妨取x0 = 0,并令g(x) = <0|x>则,
f(0) = ∫f(x)g(x) (5)
什么样的函数g能够保证,它与任意函数f的积分,永远等价于f(0)?显然,金箍棒(1)完全满足这个条件。虽然我们无法在函数的意义上严格定义g,但是,通过式(5)这种广义的积分“分布”,我们洞悉了(1)的性质,即它与任意(紧支撑)函数f的积分,只取决于f在零点的值。此时可严格定义δ函数(更严格地应称为δ分布)为:
δ[f] = f(0) (6)
虽然二十世纪三十年代狄拉克在量子物理中发现了它,并且为其引入了方便的数学符号δ,故该函数以他命名;但是我们同样需要铭记,数学家们也曾经对其做出了大量的研究,这些研究贯穿18至20世纪,包括傅里叶、柯西、基尔霍夫等人,最后在二十世纪五十年代,法国数学家施瓦茨用分布理论严格定义了δ函数。
δ函数在纯数学、基础物理和工程中都有着广泛的应用。对我们而言,它也是图像处理的基础。图像处理可看作二维的信号处理;而谈到信号处理,就完全无法离开δ函数了。
3. 线性时不变系统与卷积
如果只用一个数学概念概括早期视觉所涉及的五花八门的图像处理方法,并将它们紧紧地联系在一起,那一定是:“线性时不变系统”。
在信号处理中,有个非常重要的、称作单位脉冲响应的函数δ(k),他当然就是狄拉克函数δ,是那同一根万能的金箍棒。要讨论信号处理,首先必须表达信号。考虑一个离散的信号x(n),信号自身就能由狄拉克函数表达:
x(n) = ∑x(k) δ(n-k) (7)
式(7)显然很容易验证正确性。对于信号的输入输出,如果满足线性叠加原理,称之为线性系统,即
L(ax1 + bx2)= aL(x1) + bL(x2) (8)
其中xi表示输入信号,L(·)表示线性作用符,a、b为常系数。在一个系统中,若输入与输出之间的作用不受时间起始点的影响,称作时不变系统:
T(x(t)) = y(t)=> T(x(t- t0)) = y(t- t0) (9)
其中T(·)表示时不变作用符,x(t)、y(t)分别是t时刻的输入和输出。同时满足叠加性和时不变性原理即称为线性时不变系统。设线性时不变系统的作用符为h(·),输出为y,则:
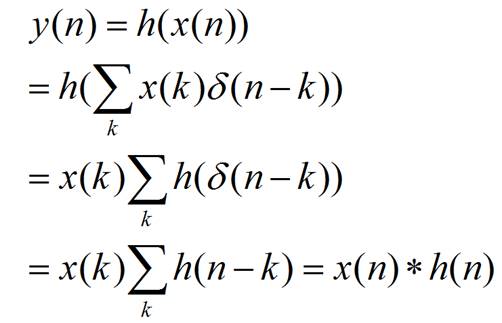 (10)
(10)
注意第三个等式用到了线性时不变系统的叠加性(将x(k)看作系数);第四个等式用到了狄拉克函数δ自身的特性;而第五个等式是我们相当熟悉的约定写法,即卷积,h(n)是系统的脉冲响应。最终,在那根金箍棒的帮助下,我们得到:一个线性时不变系统一定能由卷积表达;反之同样成立,即能由卷积表达的系统也一定是线性时不变系统。
卷积(或线性时不变系统)如何成为了图像处理的基础?又有哪些具体的应用?我们下期讨论。
后记:
这是我们第二次为一个简单的概念爬山涉水。每一个趋于实用的工程数学,都凝结着几代学者在科学道路上的闪耀智慧与辛勤汗水。回顾往昔,也是对他们的致敬与感激。对于本专业而言,数学基础已经介绍完三分之二,除了射影几何与图像处理,最后一个“观测数据的处理”将在系列(10)中介绍。
https://blog.sciencenet.cn/blog-520501-1021113.html
上一篇:澳洲点滴 (一)顺流而下