博文
摄影测量与计算机视觉 (7)几何变换的层次 下
 精选
精选
|||
摄影测量与计算机视觉
(7)几何变换的层次 下
1. 坐标系
一个物理学家,关注方程两边的量纲是否一致;一个化学家,注重等式两边是否配平;而一个几何方向的测量学家,首先要明确方程两边是否在统一坐标系下。
笛卡尔坐标系的发明,是数学史上的伟大事件。若笛卡尔的“我思故我在”消失于茫茫的哲思之海,发明坐标系的功绩也将使他英名永驻。传说笛卡尔当时正在当兵,每日在军营无所事事,幸好有个相熟的军人懂很多数学,两人相谈甚欢,笛卡尔从中受益匪浅。一日夜晚,他躺在营帐前的草地上,仰望璀璨星海。“怎么确定每颗星星的位置呢?”笛卡尔沉思良久,豁然开朗:如果用两根垂直线,就像十字架一样,悬挂天空,那么每颗星在十字架中的位置,不就确定了吗?这个瞬间idea产生的草图,最终引导笛卡尔建立坐标系。至此,几何和代数,两匹独立奔驰的骏马,将被坐标系这个强大的轭紧紧地拴在一起,诞生了解析几何;其活力进一步创造出大量的数学分支和细流。
现代数学中,笛卡尔直角坐标系由一系列相互正交的基向量表达。如三维坐标系可表达为:e1 = (1,0,0), e2 =(0,1,0), e3 = (0,0,1),那么其中的任意一个点:x = ae1+ be2 + ce3。a, b, c即该点在对应基向量上的标量投影。
摄影测量和计算机视觉中,一般只涉及二维和三维的直角坐标。而每个坐标系的建立,正如笛卡尔仰望星空:为了更加简单地描述点(星星)的位置罢了。
首先,既然图像是我们的主要观测,那么如何描述一个点(像素)在一张图像上的位置?无须从教科书中寻找干涩的定义,我们一切从头开始。很自然地,先命名一个“图像坐标系”。这个坐标系将有两个垂直的轴,分别指定为X、Y轴,其交点称为原点。根据基向量的表达形式,无论左手系、还是右手系,只要相互垂直,同样满足坐标系的定义。没关系,就分别作两个坐标系吧!图1表达了一个以左上角为原点的左手系;一个以图像中心为原点的右手系。此外,你还可以建立许许多多的坐标系,只要你愿意。当然,图1中的两个,是最方便也最常用的。
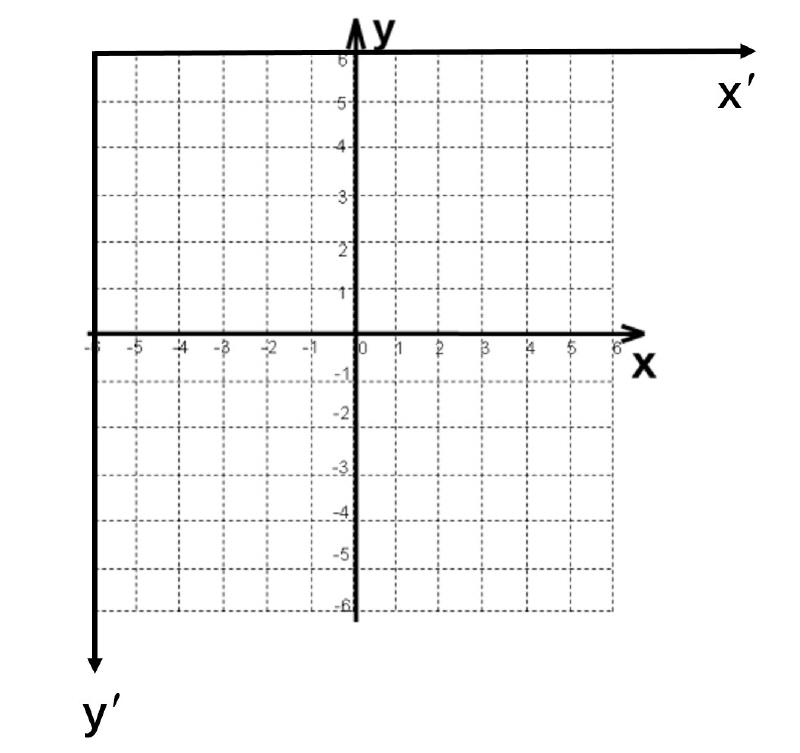
图1 x-y为右手系;x'-y'为左手系
无论如何,图像坐标系只有两个分量;而我们生活在具有三个分量的空间。正如开篇所言:要将坐标系统一起来,才能建立几何方程。故,需要将这个2D图像坐标先转换为3D坐标。为此,我们将建立第二个坐标系。最直接的方法,就是在X-Y坐标系上加上一维,按照左手系或右手系确定第三个正交分量,指定为Z轴。这样一个坐标系有着不同的名称。在摄影测量中称为“像空间坐标系”,在计算机视觉中称为“相机坐标系”。在实际应用中,往往采用右手系,并将原点移动到镜头焦点O,此时,Z轴与光轴重合。

图2 O为相机中心,O-xyz即相机坐标系,f为焦距,可见像点的z坐标永远为f。
第三个坐标系用来表达世界点的位置,称为世界坐标系。地球人自然以地球为基准。常用的坐标系包括GPS采用的WGS84、我国当前采用的国家2000大地坐标系。这是一种“地心直角坐标系”,以地球质心为原点,Z轴指向地球北极,X轴指向格林尼治子午面与地球赤道面的交点,再照右手系确定Y轴。这个“巨大”的坐标系,并不总是那么实用。如果我们只是在房间这样一个小世界,定位桌子和椅子的位置。就可以选择局部坐标系。可以选择某个墙角为原点,三根辐射线分别为X-Y-Z轴,如图3。
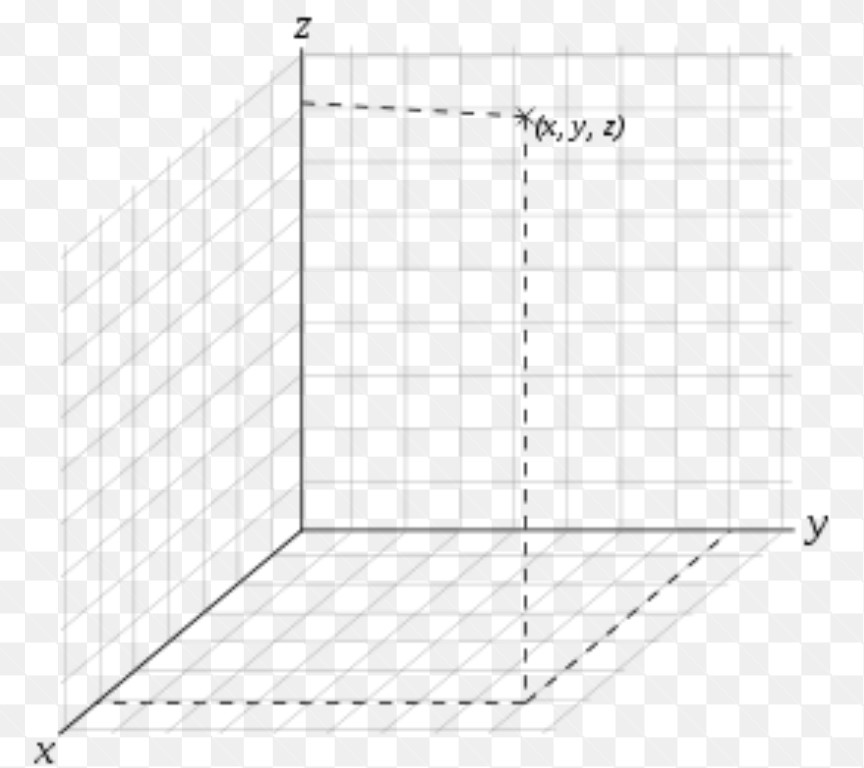
图3 以墙角建一个局部坐标系
总之,一切坐标系,以方便“几何方程的表达”为准。例如,如果相机装在飞机上、卫星上、汽车上,可以为这些摄影平台建立一个“平台坐标系”,表达相机到平台的几何关系。再如,可选择地球上的任意一点为原点,建立局部切平面坐标系。
图像上的一个点,与真实世界点,都已经用坐标系表达;那么,接下来的问题是:他们之间满足怎样的几何变换?这就需要从几何变换的层次出发。
2. 几何变换的层次
(本节公式较多,但又是几何部分的核心,也不便忽略,还请见谅。非专业的读者朋友只需要看公式11就行了:您拍了一幅照片,照片和真实世界中的您,其一一对应的几何关系就由11表达——3×3的参数K表达相机自身,3×4的参数[R|T]表达您在摄影时的pose)
先考虑同维度的几何变换。即2D与2D之间、3D与3D之间的几何变换。最简单的平面几何变换当属平移,用T表示。若加上旋转R,将构成刚体变换(或称为欧几里得变换),两个坐标系之间的变换,通常就是刚体变换;再考虑缩放λ,称为相似变换,即:
x2= λ[R|T] x1 1
这里[|]表示增广矩阵,即将两个行数相同的矩阵并列构成新矩阵。这里采用齐次式才可写成1这样的简洁形式。若采用普通坐标,则写作x2= λR x1+T。注意,在定义上,普通坐标下的相似变换并不属于“线性变换”,因此不具备线性变换的性质。1写成标量形式为:
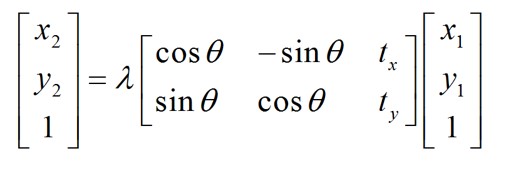 2
2
式1表达了先旋转、再平移。有时候,也可写成x2= λR(x1 - C),即先平移再旋转。两者间旋转矩阵不变,平移量存在关系:T = -RC。
相似变换共有4个参数。如果继续放宽条件,但使得平行线依旧平行,称为仿射变换。仿射变换在相似变换基础上加入了2个新的参数:
 3
3
最后,考虑最普遍的情况,令变换矩阵为3×3的任意非奇异矩阵,这时候称之为射影变换、保线变换或单应(homography),即除了直线依然保持直线外,以上性质不再成立。其变换矩阵通常用H表示,共有9个参数;但在没有更多的信息输入时,尺度是不可知的。因此可将h33设置为1,故H中有8个未知量。我们的研究对象之一就是这种平面间的变换。如对一平面摄影,物像之间需满足射影变换;同时用2台相机对同一世界平面摄影,两张图像也必须满足射影变换,即射影变换具有复合性。
 4
4
很容易推广到3D的情形。此时,平移将有3个参数,相似变换7个参数,仿射变换12个参数,而最一般的3D射影变换有15个参数。
第二步,回到我们最关心的,世界点到像片的变换,即3D到2D的变换。这类降维变换,更贴切的称谓是“投影”。
最简单的投影称为“正射投影”。设X表示3D坐标,x为平面坐标,正射投影表达为:
x = [λI|0]X 5
其中I为2×2的单位矩阵,而λ建立两套坐标系之间的比例关系。
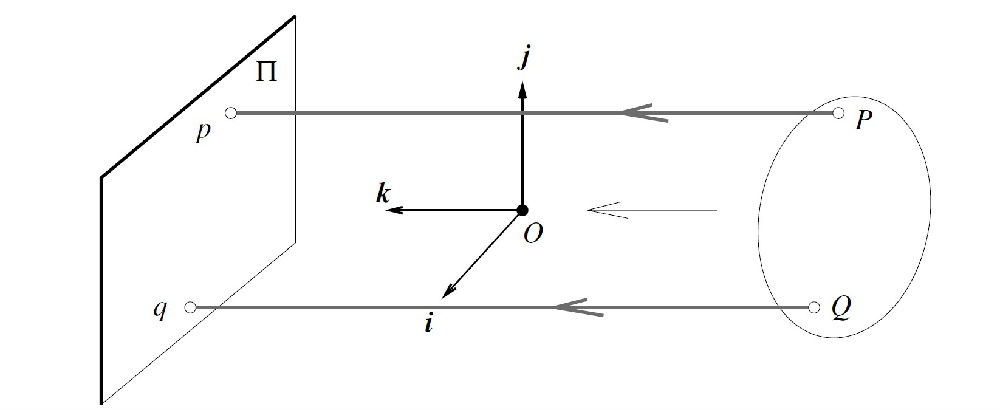
图4 正射投影
第二类常用的投影称为仿射投影。仿射投影是一种特殊的透视投影,由两步构成:物体首先平行地(可平行于物体中心与相机中心的连线)投影到与影像面平行的参考平面上;然后,再按照普通透视投影的方式将参考面投影至影像平面。两种投影联合构成了仿射投影:
 6
6
最后,被称为透视投影或中心投影的几何变换,是物体到相机最普遍的成像模型。在同一坐标系下,中心投影的公式可简单表达为:
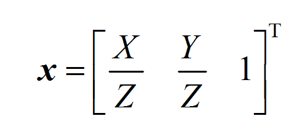 7
7
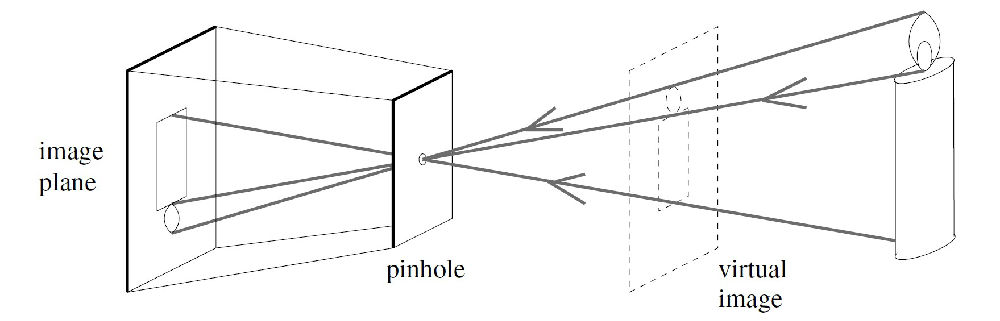
图5 透视投影(中心投影)
图像坐标一般采用原点位于左上角的左手系,物体坐标则是右手世界系,此外还可能涉及一系列中间坐标系。因此,通常物、像两者都需要经过一定的转换,使得两套观测值位于同一套坐标系下,然后再建立几何方程。这个规则同样适用于正射投影和仿射投影。首先,将图像坐标系转换为相机坐标系,并将作用于像点坐标x的几何变换参数称作为内方位元素,用矩阵K表示:
x = Kxc 8
这里的xc指相机坐标,而x是我们实际量测的像素坐标。矩阵K的参数反映在9中,共包含5个参数。s代表两个本应垂直的x-y坐标轴存在剪形畸变,通常可取s = 0。若再假设焦距fx = fy = f,这时相机参数简化为最常见的3个:坐标原点(x0, y0)和焦距f(即图2所示)。
 9
9
与此类似,X也需从所在的世界坐标系转换到相机坐标系下。两个三维空间坐标系之间的转换,就是前面已经介绍的三维刚体变换:
Xc= [R|T]Xw 10
其中Xc、Xw分别表示物体的相机坐标和世界坐标,而R和T统称为为外方位元素。现在,Xc与xc已经位于在同一坐标系中,但他们相差一个比例因子λ,联合8和10,得到:
x = λK[R|T]Xw = λX^~ 11
为消除未知比例λ,用方程组的前两行分别比上第三行:
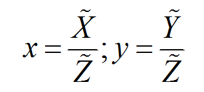 12
12
进一步地,若相机检校已经事先完成,并只考虑三个参数x0、y0、f;此时令X^-= [R|T]Xw,代入11得到:
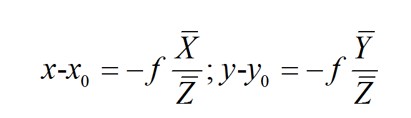 13
13
式11-13,称作共线条件方程,是整个摄影测量和视觉几何的基础。现在考虑相机参数未知的情形。根据11,将相机内、外方位元素写在一起:
P = K[R|T] 14
P称为相机矩阵(camera matrix),如果忽略比例因子,P矩阵精确表达了中心投影下物像间的几何关系;换句话说,中心投影的几何关系由相机矩阵决定。
只要理解了坐标系之间由刚体变换[R|T]决定,来再多的中间过渡坐标系也不用担心了。例如,像片是从飞机平台上拍摄的,并且世界点在大地坐标系中量测得到,那么,他们之间的关系是:
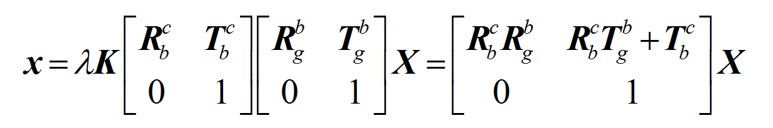 15
15
其中[Rgb|Tgb]、[Rbc|Tbc]分别是大地坐标系到平台坐标系、平台坐标系到相机坐标系的刚体变换参数。
3. 地图投影
关于透视几何的简单介绍,计算机视觉往往就在上一节结束了;但更关注宏观物体的测绘学家的麻烦才刚刚开始。无论如何,他要给公众提供各个尺度的平面地图,从全球尺度,直到一州一县。我们自然希望,在地图上所作的任何度量,能够严格保持世界的真实距离、角度、面积等属性,使得,在地图上所做的任何量测,都等价于在真实世界中的量测。事实上,在欧式空间中,等距映射(isometry)对应全等变换,已经蕴含了等角和等积在内。那么,是否有某种地图投影保证等距映射呢?
我们生活在一个不规则的近似椭球面上。远至高斯的时代,甚至更早,就已经发现,球面无法等距展开至平面,椭球当然更是如此。将一爿西瓜片拍平而保持它不破裂是不可能的。严格的证明可能要从高斯的“绝妙定理”开始。这是一个深刻的证明,虽然高斯曲率的定义需靠曲面到空间的嵌入,而最终结果却不依赖于嵌入的形式;高斯曲率可以从曲面上的长度和角度的测量完全决定。举个例子,圆柱表面和一个平面显然是3D欧式空间的不同嵌入;在圆柱上画一个三角形,将圆柱竖着裁开,就能摊成一个平面,而三角形的边长、角、面积都不发生改变;即圆柱面与平面存在等距映射。不幸的是,绝妙定理的一个推论证明:球面与平面不具备局部等距变换,地球在地图上展示时不可能无扭曲。
怎么办?既然等距变换不可行,只有退而求其次,尝试等角投影或者等积投影,并尽可能使得局部区域或 种统计意义下的形变最小。为此,高斯在1820年创立了一种现称为“高斯-克吕格”的投影(1912年由克吕格完善),将球面或椭球面投影至地图平面。这是一种保角映射。想象用一张巨大的纸卷成圆筒,将地球横着包起来,使得球面与圆柱相切于纬线;以纬线为Y轴,以赤道在圆筒上投影为X轴,按照等角投影将球上的点一一映射到圆柱上;最后再把圆柱展开为平面。为减少变形,每次只投影切线附近的局部区域到圆柱上,需要120个(若按3°带分)或60个(按6°带分)这样的圆柱。

图6 高斯-克吕格投影,分带从格林尼治开始。
另外一种常用的投影称为墨卡托投影,早在1569年,墨卡托发布了该投影下的世界地图。这是一种纵轴切圆柱等角投影。两种投影差异最大的地方在极点。墨卡托投影在极点有无穷大的面积形变。虽然高斯-克吕格投影较好地解决了极点面积形变的问题,但是,高斯投影带之间是相互分离的。这样看地图也很麻烦。
此外,还有一种通用横轴割圆柱墨卡托投影(Universal Transverse Mercator Projection,UTM)。与高斯-克吕格投影的区别在于“割”,割于北纬84度,南纬80度。而高斯-克吕格投影圆柱切于两极。
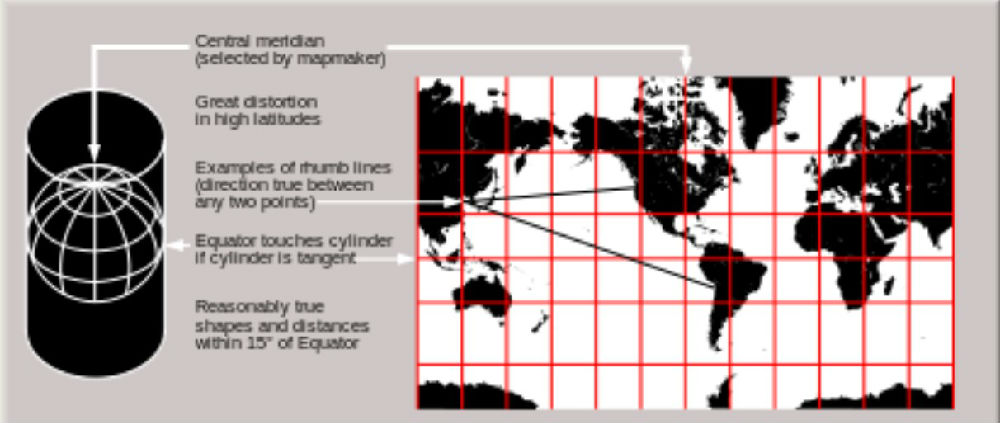
图7 纵轴切圆柱墨卡托投影
无论是横切(割)还是竖切,两种投影方式对于极点来说都不理想。球极平面投影是一种较好的针对极点的投影方式。说到极平面投影,那可要顺着时间轴一直向前回溯到喜帕恰斯(约公元前150年)和托勒密的年代(约公元100年)。那时他们已经认识到地球是个球体;而在东方,还要再等待漫长的2000年。他们两个或其中之一发明了这种投影。取一平面切于南极,从北极引射线,将球面上任意一点P(北极点除外)投影至切平面。此时,南极附近的区域,形变就很小了。同理,将切平面和投影点互换,则能得到较好的北极地区的平面投影。
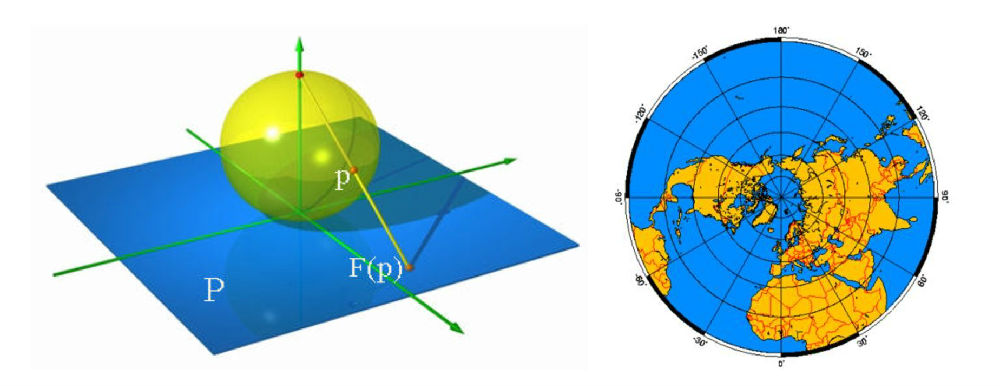
图8 球极平面投影
以上讨论了常用的地图投影。事实上,投影的概念可不仅限于将球面(椭球面)展开至平面,任何三维物体的表面都可按照一定的规则展开至平面,这也是三维重建、三维动画和游戏、虚拟现实中的关键技巧。但万变不离宗,不规则物体的投影同样无法奢望等距投影;等角投影或者等积投影则是有效的约束。其中,等角投影也称为共形映射,研究共形映射的数学叫做共形几何,目前正受到广泛的研究和应用。从规则球面到任意不规则形体,这是古老的测绘技术在现代数学和计算机技术下的升华。
https://blog.sciencenet.cn/blog-520501-1016160.html
上一篇:摄影测量与计算机视觉 (6)几何变换的层次 上
下一篇:澳洲点滴 (一)顺流而下