博文
遗失的艺术——诺谟图
|||
声明:本文主要是翻译整合了附件中的两篇英文参考文献与一些网页内容并将作为一个系列持续几篇,对诺谟图有兴趣想深入研究的的可直接查阅附件中原始文献,如果本文侵犯了相关作者的权益请留言。
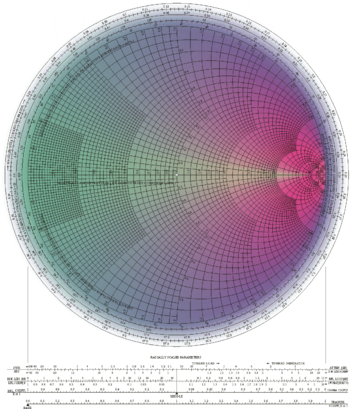
诺谟图(Nomography),又称列线图解法,于1880年由Philbert Maurice d'Ocagne (1862-1938)发明来用图形化计算解决复杂函数的求值问题。随着时代的发展逐渐淡出人们的视线,但作为人类智慧的结晶有必要将其拎出来重新讨论一下。一方面是将由计算机掩盖的一部分直观计算过程重新演绎来消除科学的神秘性,另一方面则是我个人的一种直觉:诺莫图似乎要在科学的某些领域复活并展示其巨大的威力,此外诺谟图的设计本身就是一种艺术创作,甚至同一个方程会出现两种完全不同的设计方式。
最简单的诺莫谟图是下面的温度转化图,其本质也是一个计算尺,其区别在于计算尺可通过多步计算来实现更多种类的方程计算而诺莫图则侧重于一步解决一个特殊的方程。其实诺谟图的一般形式是通过将含三个或三个以上的变量的方程中的变量用标尺表示,然后通过等值线(isopleth)将所有已知变量连接,这样未知的变量也就知道了。当然不同变量的标尺的位置是通过前期设计得到的,而这种表示方式要比3D图更为直观也易于接受。下面就开始详细介绍诺谟图的几何设计与变形

*** 几何设计
**** 平行线式
平行线式诺谟图是最简单也是最经典的一种多变量诺谟图,其基本形式与图式如下
f1(u) + f2(v) = f3(w).
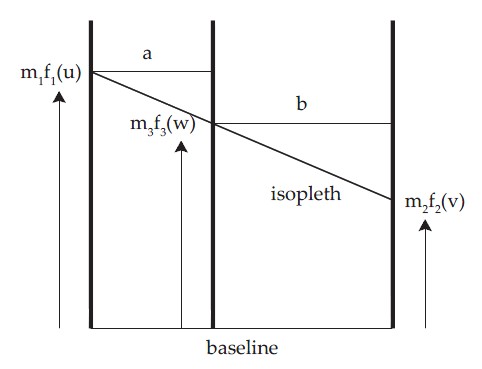
其中,m1,m2,m3代表的是比例因子,在一条等值线穿过这三条平行线后,根据相似三角形原理我们可以建立如下方程
(m1f1(u) −m3f3(w))/a=(m3f3(w) −m2f2(v))/b
整理后可得
m1f1(u) + (a/b)m2f2(v) = (1 + a/b)m3f3(w)
对照最初的基本形式,我们要做的就是消去与m、a、b相关的部分,如下
m1 = (a/b)m2 = (1 + a/b)m3
整理可得到下面的公式
m1/m2=a/b
m3 = m1*m2/(m1+m2)
好了,我们现在知道了比例因子的关系,同时我们也知道想要画的图的大小与我们关心的变量变动范围,而根据已知变量(f1(u)与f2(v))的变动范围与图的高度我们可以确定m1、m2与m3,根据m的取值与图的宽度可以定出直线f3(w)的位置,这样由于在图上f1(u)、f2(v)与f3(w)的坐标都是线性均匀分布的,现在就可以用等值线来进行求解了。
也许看到这里你会说求个线性方程费这么大的劲是没意义的,但线性方程可不仅仅就这一种形式,原则上可以转化为线性方程的方程都可以用诺谟图来求解,例如下面的两种转化
log (cd) = log c + log d
log (c^d) = d log c
其实,这样做的同时你也会发现标尺不再是均匀的了,但没关系,因为我们在绘图时依然可以采用均匀的标尺,然后附加一个对数表就够了,要是有耐心可以把标尺按原始数据绘制上去,这都不影响我们计算的准确性。
***** 实例
上面的理论分析太过枯燥,下面我们用一个例子来展示在处理复杂的工程经验方程时诺谟图的绘制。方程如下
(1.2*D + 0.47)^0.68*(0.91*T)^(3/2) = N
我们关心的范围是1.0<D<8.0与1.0<v<2.0,而u与v的长度都设置为11cm而宽度设置为6cm,首先进行方程变形
0.68 log(1.2D + 0.47) + 1.5 log T = logN − 1.5 log 0.91
然后根据图形长度范围与参数范围求解m
m1 =11/(0.68 log(1.2(8.0) + 0.47) − 0.68 log(1.2(1.0) + 0.47))= 20.73
m2 =11/(1.5 log 2.0 − 1.5 log 1.0)= 24.36
m3 = m1*m2/(m1 +m2)= 11.20
根据宽度范围求解第三条线的位置
a/b= m1/m2= 0.851, a = 0.851b;
a + b = 6, 0.851b + b = 6
b = 3.241 cm a = 2.759 cm
好了,我们开始画图
在D轴上我们的起始点是1.0,然后按照下面的公式在11cm的范围中求坐标
20.73 *(0.68 log(1.2D + 0.47) − 0.68 log(1.2(1.0) + 0.47))
然后画出T的范围,起始点依旧是1.0。坐标公式如下
24.36(1.5 log T − 1.5 log 1.0)
最后我们距离D轴2.759cm处垂直基线画一条N轴,起始点通过下面公式求出
(1.2(1.0) + 0.47)^0.68*(0.91(1.0))^1.5 = 1.230
坐标通过下面公式求出
11.20*(logN − 1.5 log(0.91))
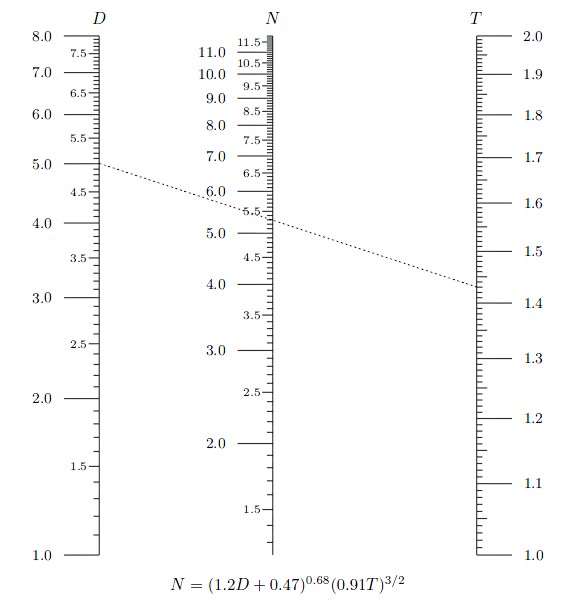
OK,现在我们可以得到这张诺谟图了。并且现在我们可以看出诺谟图在求解复杂方程上是很方便的,甚至可以求解一些无解析解的方程。
网络资源
这个坑我挖的太大了 都过去一年半了 后半段(基本就是展示 基本原理就在上面)通过evernote将其在左侧微博上共享链接
http://www.evernote.com/shard/s41/sh/aa5553d3-dfa8-44b9-afe8-517d65ed867f/96123b8462ca55eec8feae244ca7896d
https://blog.sciencenet.cn/blog-430956-459172.html
上一篇:《量子物理史话》读书笔记
下一篇:太阳能的潜力有多少?
扫一扫,分享此博文
全部作者的其他最新博文
- • 双城记
- • 研究速递(2023年下半年)
- • 数据量是否越大越好?
- • 可以不知道
- • 诺奖得主侃大山
- • 有人生环