博文
基于物质运动新描述的剪切波解释--论证剪应力不互等
|
本人自2019年7月开始了解到部分研究者对剪应力互等的质疑并接受剪应力不互等这一观点,随后开始尝试论证剪应力不互等。至今历时15个月有余,本人自认为通过对剪切波的解释论证了剪应力不互等的观点。但需要指出对剪应力互等的挑战就是对牛顿三定律普适性的挑战。近一年在科学网上看到不少博文对连续介质力学中的剪应力互等提出了质疑,当然也有学者发表对剪应力互等表示认同的见解。这里也来凑个热闹。本人不敢与神相争,下述陈述仅作闲谈。
牛顿力学认为宏观物质的运动可看作质点系运动的集合。客观世界质点是不存在的,构成宏观物体的微元依然是有体积的。本人认为微元的转动是否可忽略不依赖于微元的大小而是依赖于所研究的问题。因此,牛顿三定律是忽略微元转动而只考虑平动时的运动定律。本人认为剪切波位移场为旋度场,剪切波对应的应力与局部刚体转动有关说明了:剪应力互等和微元体的质点描述不客观。因此,本人建立了微元体绕质心转动的动量矩守恒方程,相应地修正了应力应变关系,给出了和现有波动方程完全相同的波动方程。
当然仅说自己的模型可以推导出剪切波方程并能合理解释剪切波是远不够的。让大家接受下面观点还需指出传统波动方程的推导错哪里。这里先推荐大家看一下邱泽华老师的书籍《非对称线弹性理论》中第一章的观点。本人的观点是在其基础上说明剪切波的定义是如何打破剪应力互等的。下面(下图)是对反平面剪切波的定义。可以看到反平面剪切波的定义只告诉我们沿x3方向的位移和应力不为0,其它方向的位移为0,但应力未做说明。因为在波动方程的建立过程中都未用到其他应力分量,因此本人认为其他方向的剪应力为0,剪切波的定义打破了剪应力互等。其实从下面应力应变关系(2.54)也可以看到剪切波的定义已经考虑了局部转动对应力的贡献。我想这再一次说明剪切波的定义以打破了剪应力互等和微元体的质点描述。即从只考虑微元体平动的质点运动描述无法得到剪切波方程。

弹性理论是小变形,满足叠加原理。下面我们基于微元体转动建立剪切波波动方程。只有作用于弹性体的外力的环量不为0时,物体才会转动。因此弹性体动量矩守恒的积分形式应表示为如下形式:
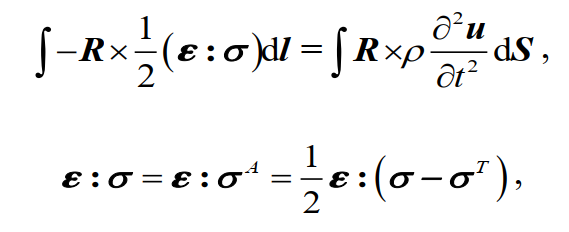
利用Stokes理论,上式可用微分形式表示为:
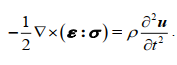
下面我们修正应力应变关系。我们已经打破了剪应力互等,因此剪应变互等也就不成立了。反对称应力应来自于反对称应变(或称作变形)。因此位移梯度的反对称部分也应贡献应力,应力应变关系应表示为如下形式:
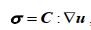
即连续体不发生宏观转动时,变形由位移梯度表示。对于各向同性弹性体,弹性张量C应表示为:
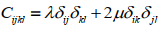
此弹性张量与传统表示不同。弹性理论已经声明过应变张量为对称张量,传统弹性张量只是保证应变张量写错(不对称)时,应力张量依然为对称张量。因此传统表达事实上显得多余。本人认为传统弹性张量可由上式代换。如果我们将修正的应力应变关系带入微元体转动方程,便可得到:
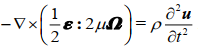
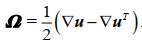
由于下式成立:
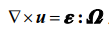
我们便可得到传统的剪切波方程:
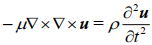
利用叠加原理可进一步得到弹性体的波动方程:
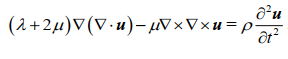
本波方程与传统波动方程完全相同。不同之处在于此时纵波方程对应微元体平动动量守恒方程,剪切波方程对应微元体绕质心转动的动量矩守恒方程。纵波和剪切波的位移场常会用标量势和矢量势函数表示。在微元运动的体刚体描述时,纵波的应力场为散度场,位移也是散度场;剪切波的应力场为旋度场,位移场也是旋度场。即散度的归散度,旋度的归旋度。从这一层面看将弹性体微元的运动描述为刚体运动似乎是更合理的,物理意义也更明确。因此,本人自认为自己想法是正确的。
上面的波动方程的推导打破了物质运动的质点描述,因此也就挑战了牛顿三定律的普适性。连续介质力学的运动描述建立在微元体的质点描述之上,接受上述观点也就意味着连续介质力学的基础被否定了。Navier-Stokes方程(被认为是牛顿流体运动终极描述者)也自然(大概率)不可能准确描述牛顿流体的运动。这里附加一句,本人不认为将流体微元的运动换成刚体运动就能获得正确描述流体运动的方程。作者更相信上帝也不懂流体。
目前有不少研究者在传统连续介质基础上想引入微元体转动,如偶应力理论。但似乎他们也只是在连续体的本构关系上做文章。在描述微元体运动时,却还是不敢越雷池半步。这让我觉得偶应力理论的理论基础是前后矛盾的。考虑微元体转动并建立微元体转动方程,偶应力理论或可用夹杂思想去描述。
最后结语:上述观点纯属一家之言,肯定存在不少错误结论。论断仅供参考,不可过于认真。
全文可参见如下链接(论文预印本):https://arxiv.org/abs/2005.13145
Derivation of wave equation from new motion description
https://blog.sciencenet.cn/blog-3439201-1256923.html
下一篇:连续介质力学算科学吗