众所周知，希尔伯特《几何基础》（以下简称“希著”）没有空间顺序定理或者公理，只有直线和平面上的顺序公理，其中平面上的顺序公理即所谓帕施公设。本文试对空间顺序定理进行证明。证明过程除用到帕施公设外，主要用到了希尔伯特公理体系的结合公理。

　　下面先给出所用公理：

　　若两平面α、β有一个公共点A，则一定还有另外的公共点B——I₇。（在此基础上可以得出下面命题：两平面或无公共点，或有一公共直线，无公共直线时无公共点。此为希著定理1）

　　设A、B和C是不在同一直线上的三点：设a是平面ABC的一直线，但不通过A、B、C这三点中的任一点，若直线a通过线段AB的一点，则它必定也通过线段AC的一点，或线段BC的一点。——II₄，即帕施公设。

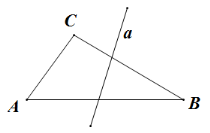
　　下面我们进行证明：

　　已知：A、B、C、D是不在同一平面上的私点，设l是一直线，但不通过这四点及这四点的连线，直线l通过三角形BCD内部一点.

　　求证：直线l必定也通过三角形ABC、ACD、ADB的一点。

　　证明：

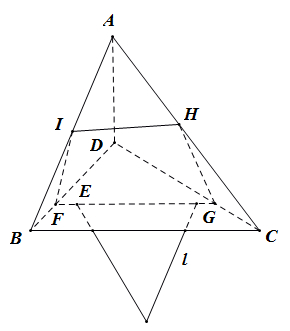
　　在平面BCD上任取一点E，过点E和直线l作平面。

　　因为此平面与BCD有交点，所以一定存在交线。【前述定理1】

　　延长交线，设其与BD交于点F。

　　又根据II₄，这一直线若经过边BD，则一定与BC、CD之一相交。设其与CD相交于G。

　　即直线FG即是交线。

　　又，所作平面既然与ABD交于F，则一定与ABD有交线，且根据前面类似的理由，设所作平面与ABD交线为FI，其中点I是所作平面与AB或AD的交点。（图中点I在AB上）

　　类似可以证明，所作平面与AC或AD也有交点，设其为H。（图中点H在AC上）

　　所给直线l在所作平面上，而所作平面与四面体的交线分别为FG、GH、HI、IF，且其中FG是所作平面与BDC的交线。

　　连接GI。

　　如果直线l与FI相交则得证，否则，根据帕施公设，直线l一定与GI相交。

 　　再根据帕施公设，直线l一定与GH、HI之一相交。

　　得证。