博文
刘瑞祥:欧几里得《原本》一命题的别证
||
提要:
“第五公设”(平行公设)是欧几里得《原本》(文献1)中的一个热点问题,这一问题随着非欧几何的建立而从原则上获得了解决,但对于每一具体问题来说,还需要更深入的分析。本文对《原本》中一个命题提出另外的证明方法,试图使之摆脱第五公设。
正文:
文献1对于第五公设(文献1,P2)的态度是“能不用尽量不用”,这不但表现在它直到第一卷的命题29才用到这一公式,更突出地表现在第一卷命题16(三角形的外角大于内对角,文献1,P15)、命题26(三角形全等判定定理角边角及角角边,文献1,P23)第三卷命题17(由已知点作直线切于已知圆,文献1,P78)中没有用到第五公设及其等价命题上,尽管如果用第五公设则角角边定理是角边角定理的直接推论。
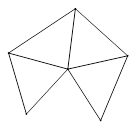
细查不需要第五公设的命题,可以将其分为几种类型,其中之一是涉及不等量的关系的。因此,其第11卷命题21——构成一个立体角的所有平面角的和小于四直角(文献1,P525)——用到了“三角形内角和为二倍直角”这一间接涉及第五公设的命题作为依据就显得相当奇怪。这一命题的直观形象是,将一个棱锥的侧面沿着侧棱剪开后铺成平面,不会铺成一周,总会留有空隙:
文献2对上述命题给出了一个新的证明:
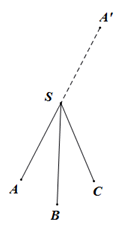
S-ABC是一个三面角,延长SA为SA'(于是两个半面SAB和SAC补足到它们的交线SA')形成了一个新三面角S-A'BC。在这新三面角中有 ∠BSC<∠BSA'+∠A'SC或∠BSC<4d-∠ASB-∠ASC。(d为直角,其中∠BSA'=2d-∠ASB,∠A'SC=2d-∠ASC。) 由此式得∠BSC+∠ASB+∠ASC<4d。 |
这里唯一用到的一条依据是如下命题:如果由三个平面角构成一个立体角,则任意两个平面角的和大于第三个平面角(文献1,P524),而这不需要第五公设。
文献2还对更多平面角组成的多面角的情况进行了简单叙述,但没有给出详细证明,下面本文就对在前面的基础上作进一步证明,即任意的凸面角的平面角之和小于四倍直角。
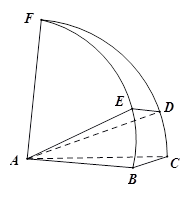
以四个平面角组成的多面角为例: 以多面角的顶点A为球心,任意长为半径作球,多面角的各个棱交球面于点B、C、D、E, 因为各个平面角的顶点都是A, 所以任意两个平面角所在的平面(无论是否相邻)都有交线。(两平面相交于一点,则一定交于过这点的直线) 设夹某平面DAE的平面BAE、CAD的交线为直线AF, 又设平面ABE与球面交线为弧BEF,平面ACD与球面交线为弧CDF。 因为∠BAC+∠BAF+∠CAF<4d,(前引文献2的证明) 而其中∠BAF=∠BAE+∠EAF,∠CAF=∠CAD+∠DAF, 所以,∠BAC+∠BAE+∠EAF+∠CAD+∠DAF<4d。 又∠DAE<∠EAF+∠DAF,(文献1) 所以,∠BAC+∠DAE+∠BAE+∠CAD<4d。 更多平面角组成的多面角可用类似方法逐步化成凸四面角。 |
众所周知,第五公设的应用范围很广,有时也很隐晦。笔者前面所证的过程很可能不经意地间接用到了第五公设。以上内容敬请专家读者指正,即使最终这一命题还是离不开平行公设,以上也算是对之给出了另外的证明方法。
参考文献:
1:欧几里得,《欧几里得几何原本》,兰纪正、朱恩宽翻译,陕西科学技术出版社2003年出版
2:J.阿达玛,《几何 立体部分》,朱德祥译,上海科学技术出版社1966年版
https://blog.sciencenet.cn/blog-3388899-1140078.html
上一篇:刘瑞祥:三角形全等命题之ASS成立的几种情况
下一篇:刘瑞祥:科学知识的有用和无用
全部作者的其他最新博文
全部精选博文导读
相关博文
- • AAA PCI -- 学者心声(Authorea 预印论文报道)
- • Building a DIKWP-TRIZ Software System (初学者版)
- • DIKWP-TRIZ: Semantic Blockchain and Semantic Communica(初学者版)
- • DIKWP-TRIZ in 3-No Problem and Artificial Consciousnes(初学者版)
- • Comparison Between DIKWP-TRIZ and TRIZ(初学者版)
- • DIKWP-TRIZ: Enpower AI/AC Innovation (初学者版)