博文
应用统计学与R语言实现笔记(番外篇三)——缺失值的相关系数分析
|||
昨天刚好有位同学来咨询R语言里计算相关系数的一些问题,所以来谈谈关于缺失值的相关系数分析问题,主要是在R语言中如何处理含缺失值数据的相关系数分析。
1 问题描述
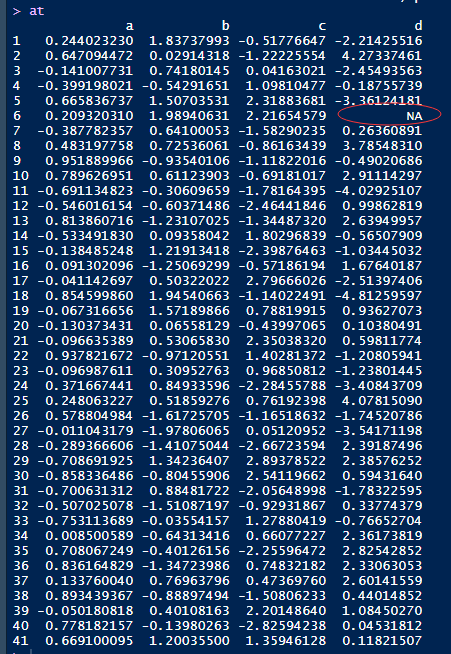
相关分析可以说是数据分析以及探索性分析的基础。一般拿到手的数据,起手先来一波相关分析。同学遇上的问题如下:类似如下的数据。这里的数据是我利用随机分布随机造出来的,跟我同学的数据的一些基础分布特征是相似的。其实关键就是第四列数据有缺失数据。
然后在计算具体的相关系数时发现了一些问题。
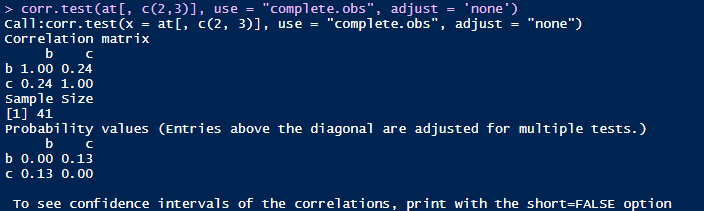
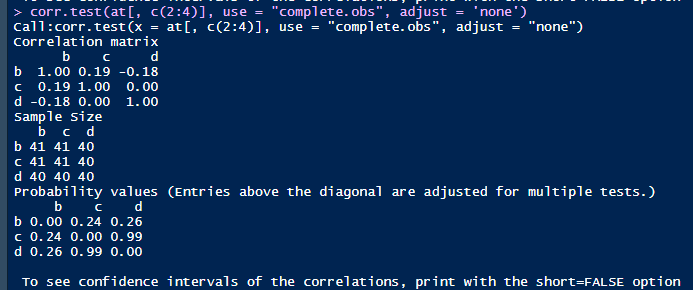
可以清楚地看到在只计算b和c的相关系数的情况下,相关系数与p值分别为0.24和0.13,但当b,c和d都参与运算的情况下,相关系数和p值就变成了0.19和0.24。造成差别的原因是什么呢?
2 R语言相关分析中的缺失值处理原理
经过检查,关键在于use的参数的选择。use可以设置的参数主要包括pairwise,complete,complete.obs,pairwise.complete.obs,everything等。这里分别来看具体的含义。事实上这些都是针对相关系数公式里的协方差计算的设置。
- pairwise:使用成对样本计算。
- complete/complete.obs:必须选择完整的样本计算,目前没发现这两个有什么区别。
- pairwise.complete.obs:通过在成对的基础上省略具有缺失值的行而形成的向量为每对列计算相关性。
- everything:不对缺失值做任何处理,因此缺失值结果会直接传递给相关系数矩阵与p值计算。也就是说含有缺失值NA的变量无法计算出相关系数与p值。
由于前面提到这是针对协方差的计算,所以可以再查看R里面计算协方差的函数——cov的帮助文档协助理解。这是原文。
If use is “everything”, NAs will propagate conceptually, i.e., a resulting value will be NA whenever one of its contributing observations is NA. If use is “all.obs”, then the presence of missing observations will produce an error. If use is “complete.obs” then missing values are handled by casewise deletion (and if there are no complete cases, that gives an error). “na.or.complete” is the same unless there are no complete cases, that gives NA. Finally, if use has the value “pairwise.complete.obs” then the correlation or covariance between each pair of variables is computed using all complete pairs of observations on those variables. This can result in covariance or correlation matrices which are not positive semi-definite, as well as NA entries if there are no complete pairs for that pair of variables. For cov and var, “pairwise.complete.obs” only works with the “pearson” method. Note that (the equivalent of) var(double(0), use = *) gives NA for use = “everything” and “na.or.complete”, and gives an error in the other cases.
整体说起来还是比较抽象。往下我们可以通过一些简单的R语言计算来进行协助理解。当然这个案例并非我独创,我在谷歌上做了相关搜索,发现了一个关于描述这个相关系数计算处理缺失值非常不错的网页。我相当于是翻译+搬运工。
3 “Pairwise-complete correlation considered dangerous”案例
网页标题为“Pairwise-complete correlation considered dangerous”,翻译过来就是成对完全相关分析可能造成一些错误结果,作者为B. W. Lewis。
这个案例首先构造了一个数据。3列 x 5行的矩阵,其中第三列的第一行和第二行矩阵元素是缺失值NA。
x <- matrix(c(-2,-1,0,1,2,1.5,2,0,1,2,NA,NA,0,1,2),5)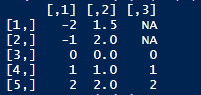
接下来我们分别用不同use的参数设置来查看结果。这里作者原文使用cor函数,但是我们前面的案例是使用pysch的corr.test函数,这里就还是采用这个函数进行对应计算。而由于corr.test()对矩阵的计算似乎不是很友好,我们做个类型转换,将矩阵转为数据框,也就是R语言的data.frame。
#数据转换xu <- data.frame(x)
colnames(xu) <- c("a", "b", "c")#计算对应的相关系数矩阵corr.test(xu, use = "everything", , adjust = 'none')
corr.test(xu, use = "pairwise", adjust = 'none')
corr.test(xu, use = "complete.obs", adjust = 'none')
corr.test(xu, use = "pairwise.complete.obs", adjust = 'none')use等于everything时候的输出结果。所谓的传播就是,含有NA的第三列与第一列和第二列的相关系数只能为NA,只要数据有NA就无法计算像相关系数。
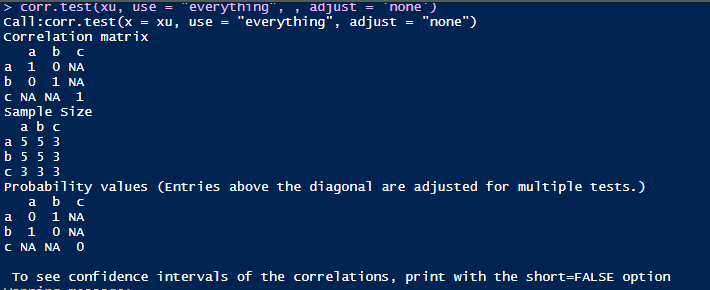
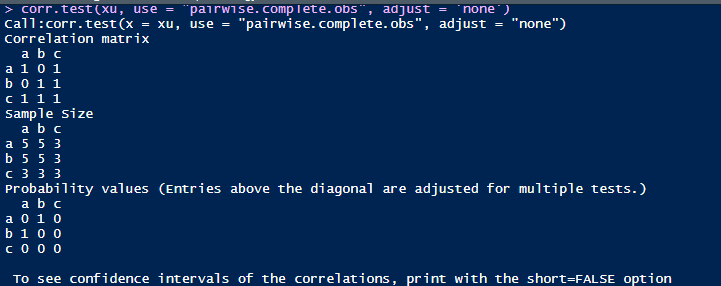
use等于pairwise时候的输出结果,可以发现a和b的相关系数为0,a,b和c的相关系数为1。那么我们来解析下具体的计算。
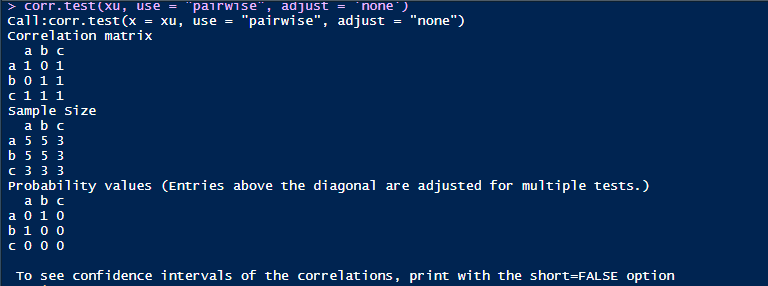
相关系数的公式如下,然后可以计算下5个样本下的协方差和并且绘制散点图。
$$
plot(xu[,1], xu[,2], xlab = "a", ylab = "b", col = 'red', pch = 16)
cov(xu[,1], xu[,2])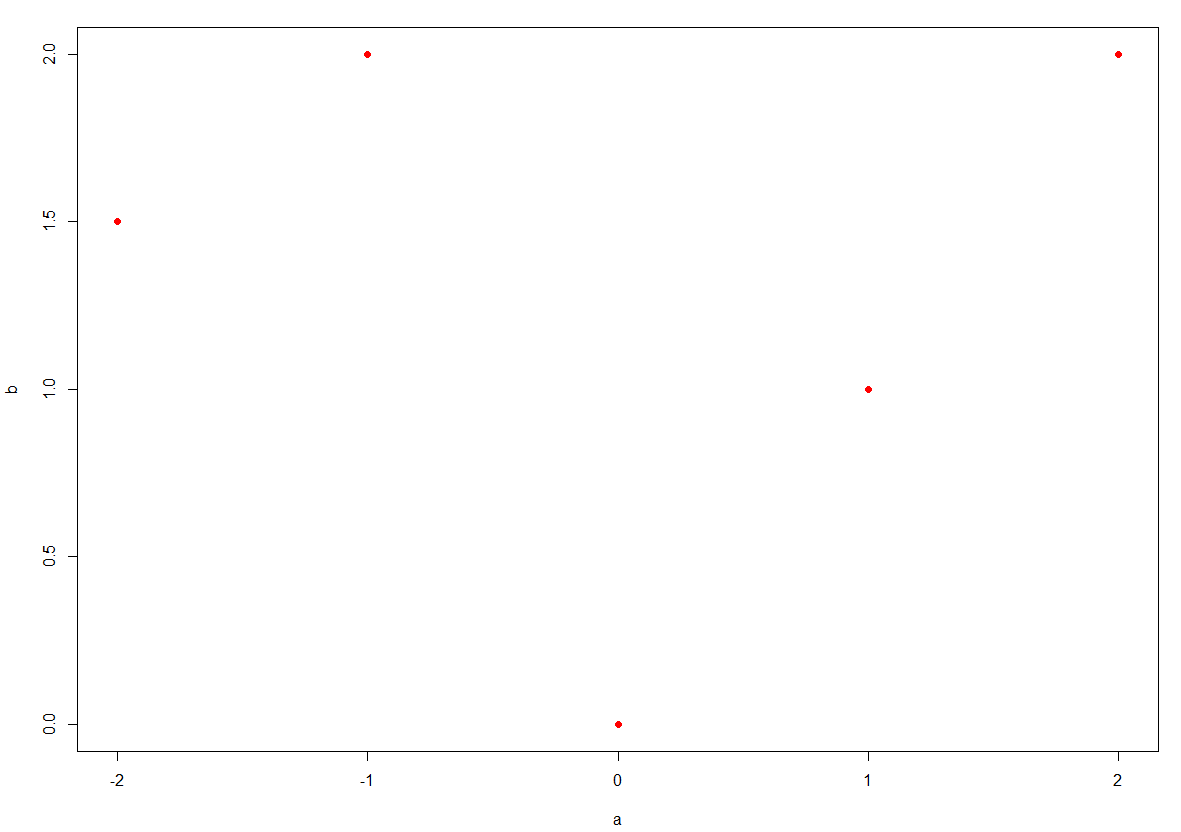
协方差为0,所以相关系数为0。这就得到结果了。

pairwise计算的方式如下:由于a和b是没有任何缺失值,5个值可以完全配对,所以在计算的时候a和b的相关系数是基于这5对数据计算,而对于a和c以及b和c的相关系数计算,由于c有缺失数据,可以完全配对的数据仅有三对,仅仅基于这三对配对样本计算相关系数。这样子对应计算出来的相关系数就是1了,因为这些数据完全一致。因此就像Lewis先生说的一样,由于在计算相关系数的时候,样本不统一(在本案例中a和b的相关系数计算是5对配对样本,a和c以及b和c的相关系数计算是3对配对样本),事实上这样计算的相关系数不具备可比性,也可能混淆原来数据的关系。
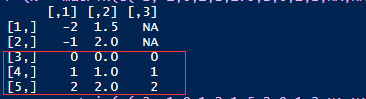
现在我们再来看complete.obs,可以发现这是a,b,c的相关系数全为1。这是怎么计算出来的呢?根据对数据的观察可以发现,矩阵数据的第三到第五行的每一列数据都是相同的。

complete.obs的计算方式:由于c有缺失数据,在计算前必须去除掉所有NA的行,也就是去除掉第一行和第二行的所有数据再进行相关系数的计算。这样子所有a,b,c三个变量都仅有3个数据。而且是全部一致的变量。因此这就是完美的完全相关(r=1)。
至于pairwise.complete.obs结果与pairwise是一样的结果,我目前没有发现太大的差别。
因此正如Lewis先生说的,有时候完全匹配样本的分析反而容易造成对数据的曲解。当然最好的方式是获取更多的观测样本。
最后回到同学的数据,为什么只针对b和c做相关分析的结果与针对b,c,d做相关分析的时候,b和c的相关系数有差异呢?
我们可以看到存在差异的语句是由于使用了complete.obs,因为complete.obs会删除NA数据,当仅针对b和c做相关分析的时候,不存在NA数据,所有是针对所有41个数据计算得到的相关系数。而由于d存在NA数据,在对b,c和d做相关分析的时候,必须删除那一列,所以b,c和d都是仅剩下40个数据计算得到的相关系数。所有有差异是可以理解的。而当采用pairwise的时候,即使有NA数据存在,b和c的相关系数计算也不会因为有NA而去除掉b和c对应的那行数据,所有前后样本数据量一致,相关系数自然不会有变化。
另一个角度反应出来,d那一行的数据对这三个变量的数学关系影响还是比较大的,因为有些情况随机模拟出来的数据,也不一定会有明显的相关系数差异。因此针对缺失值如何处理还是要根据数据具体情况而言。由于我之前通常在相关分析前就去除了NA值,所以我也没遇到过这个情况。这其实是非常有意思的统计分析诊断。
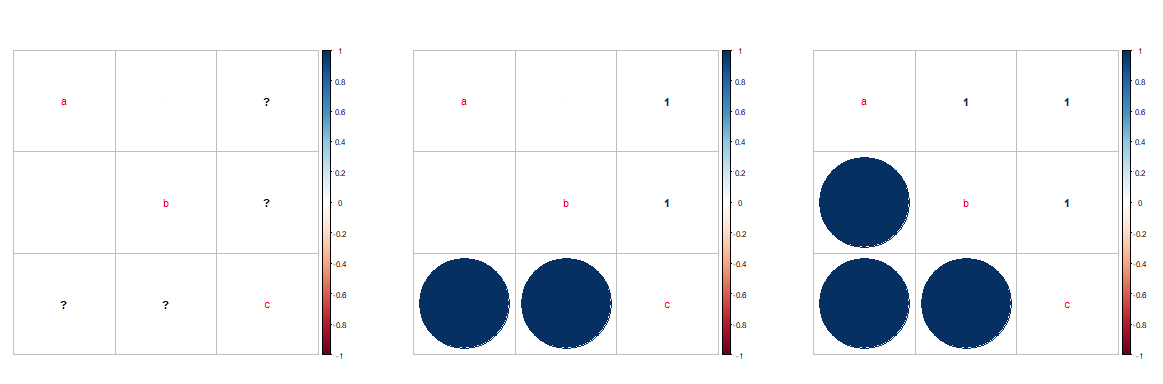
相同数据,不同use方法的相关系数矩阵可视化。

本文使用的代码,我会放到我应用统计学与R语言实现笔记的开源github仓库上,有兴趣的同学欢迎自行下载。
Note-of-Applied-Statistics-with-R
参考链接:
https://blog.sciencenet.cn/blog-3247241-1226067.html
上一篇:葵花8号卫星数据简介与下载(一)
下一篇:R语言实现voronoi treemap可视化
全部作者的其他最新博文
全部精选博文导读
相关博文
- • AAA PCI -- 学者心声(Authorea 预印论文报道)
- • Building a DIKWP-TRIZ Software System (初学者版)
- • DIKWP-TRIZ: Semantic Blockchain and Semantic Communica(初学者版)
- • DIKWP-TRIZ in 3-No Problem and Artificial Consciousnes(初学者版)
- • Comparison Between DIKWP-TRIZ and TRIZ(初学者版)
- • DIKWP-TRIZ: Enpower AI/AC Innovation (初学者版)