博文
近场动力学最新上线的文章快报:2020年6月(上)
|
每期文章评述的首发平台是微信公众号:近场动力学PD讨论班,也可以搜索微信号:peridynamics,或扫描文末的二维码加入。
2020年6月上期近场动力学领域有六篇新文章上线。本期可谓篇篇精彩:文一针对双相材料的塑性变形与渐进损伤预测进行建模并与实验观察进行了对比;文二针对脂质膜上夹杂物的弹性和熵相互作用进行了研究,所提出的模型可以用于探讨不同膜几何形状对膜的夹杂物相互作用的影响;文三提出了用于模拟大变形和延性断裂的键型半拉格朗日近场动力学方法,显著提高了对延性断裂的预测精度;文四提出了一种键型近场动力学的全耦合流体力学模型,用以模拟裂隙多孔岩中的加压和流体驱动压裂过程;文五针对可固化聚合物的挤压成型增材制造工艺进行了建模与模拟;文六借助分子动力学构建了界面材料的本构关系,提出了用于模拟颗粒增强金属基复合材料的近场动力学模型,成功应用于该复合材料准静态问题和动态问题的研究。下面我们依次简要介绍: 文一: https://doi.org/10.1016/j.engfracmech.2020.107179 双相材料塑性变形和渐进损伤预测的近场动力学微力学建模 本文建立了态型近场动力学微结构模型,用于模拟多相材料中的损伤起始、扩展以及塑性变形。将双相钢作为研究的材料实例,作者们建立了二维近场动力学模型来预测三种代表体积元在静态拉伸荷载作用下的响应。通过图像处理从扫描电子显微镜图像中提取代表体积元。在模拟塑性变形时,采用了Von Mises硬化屈服准则。本文通过将消除相互作用的近场动力学总功与临界能量释放率关联起来建立失效准则。除此之外,本文还提出了一种新的边界条件和分配界面区域属性的方法。材料的一些失效机制,例如,马氏体开裂、铁素体和马氏体界面脱粘,均可被该模型捕捉到。本文还发现损伤起始发生在马氏体晶粒的窄截面、铁素体/马氏体界面和俘获的铁素体相中。作者们将本文预测的变形、应力-应变曲线和损伤模式也与现有的实验结果进行了比较,所得的预测结果与实验吻合较好。 图:马氏体相,边界(a-e),和铁素体相(f)的孔洞成核。 图: 分别由 (a) 马氏体开裂,(b) 铁素体/马氏体界面脱粘,引起的空洞成核。 图:三种代表性体积元的损伤扩展。 文二: https://doi.org/10.1016/j.jmps.2020.104046 计算脂质膜上夹杂物弹性和熵相互作用的近场动力学方法 脂质膜上夹杂物相互作用背后的物理机制与调节细胞的胞外胞内作用的蛋白质的自组装有关。由于含有夹杂物的脂质膜其势能可以用包含面内张力和面外挠度耦合的刚度矩阵表示为二次形式,因此这些相互作用可以用高斯积分计算的自由能变化来量化。自由能计算需要计算出当前能量表达式中的刚度矩阵的行列式。然而,该刚度矩阵的大小由脂质膜及其分子组成的特征长度尺度决定,以至于要计算一个极大的刚度矩阵的行列式,这给计算带来了挑战。本文提出了一种近场动力学方法来构造刚度矩阵,并在不增加任何计算难度的情况下准确地计算其行列式。该方法特别使用了配分函数计算中的关键步骤——近场动力学微分算子来准确计算刚度矩阵的行列式。本文同时使用细网格和粗网格以及近场动力学插值消除了网格间距减小带来的计算挑战。通过再现波动弹性杆的蠕虫链模型(一种DNA环化模型)力-伸长关系来说明这一点。对于没有任何夹杂物的薄膜,随着网格间距的减小,近场动力学的预测解收敛并逼近于薄膜张力-面积关系的解析解。在存在夹杂物的情况下,近场动力学预测解捕捉到了膜的预期变形以及不同夹杂物间距、形状和位置下的相对自由能行为。本文发现相对自由能的大小随着夹杂物数量的增加而增大,这表明在较大的团簇中相互作用程度较高。本文提出的方法具有通用性,可以探讨不同膜几何形状(膜曲率、边界条件和膜与夹杂物的接触角)对膜的夹杂物相互作用的影响。 图:静水压力下含有夹杂物的薄膜。 图:含有夹杂物的薄膜:(a) 颗粒聚集情况1,(b) 颗粒聚集情况2。 图:颗粒聚集情况1含夹杂物薄膜在s=50nm时的变形构型。 文三: https://doi.org/10.1007/s10704-020-00455-1 重温第三次桑迪亚断裂挑战赛:模拟大变形和延性断裂的键型半拉格朗日近场动力学方法 在最近参加完2017年桑迪亚断裂挑战赛之后,作者们发现了近场动力学理论在预测大变形和延性断裂方面的一些缺点,并且提出了一个键型、半拉格朗日近场动力学模型来解决这些缺点。这一新理论被用来重新审视这一挑战问题。作者们的计算结果表明,在这一挑战赛中,新的方法显著提高了对延性断裂现象的预测精确性。 图:断裂挑战的几何模型示意图(左图为表面图,右图为剖面图),挑战问题中局部应变跟踪的参考位置为(P1-P4, H1-H4),位移测量位置为(P5-P10)。 图:在裂纹萌生(a, b)和完全失效(c, d)时,实验DIC测量和近场动力学模拟的垂直Hencky应变云图对比。 文四: https://doi.org/10.1016/j.ijrmms.2020.104383 裂隙多孔岩中加压和流体驱动压裂过程的流体力学键型近场动力学模型 本文提出了一种新的关于键型近场动力学的全耦合流体力学模型,以模拟裂隙多孔岩中的加压和流体驱动压裂的过程。作者们基于经典的BIOT孔隙弹性理论,建立了裂隙多孔岩体的模型。耦合的流体-力学键型近场动力学模型包括两部分:流体流动和力变形。作者们根据所建立的流体流动的控制方程,同时建立了应用于裂隙多孔介质的积分-微分运动方程。此外,作者们还在流体力学的近场动力学模型中引入断裂准则,以模拟高流体压力引起的破坏。最后,进行了四个算例的数值模拟,以验证所提出模型的准确性和正确性。 图:孔隙岩石试样中流体注入驱动的两个裂隙之间的裂缝扩展和合并示意图:(a)几何形状和边界条件; (b)损伤分布和(c)流体压力分布(单位:Pa)。 图:试样的裂纹扩展过程(左)和流体压力分布演化(右)。 文五: https://doi.org/10.1007/s40571-020-00337-2 应用近场动力学对软质聚合物增材制造进行数值模拟的固化模型 本文提出了可固化聚合物基于挤压增材制造(AM)工艺的建模和模拟。AM的挑战在于对工艺参数的调校。这包括应用激光照射到达局部的加速固化,从而控制植入物的最终几何形状。由于凭借操作员的经验很难预测复杂的多物理场耦合效应,因此数值模拟是一种有帮助的预测手段。当仿真能准确地把握AM工艺的基础物理效应时,就有可能对该工艺真实地表征。为了对工艺中的材料行为进行建模,作者们建立了过程依赖的大应变固化模型,并考虑了材料的无应力固化行为。目前现有的模型还无法模拟低固化聚合物的流体行为,它需要一个考虑了有限变形的公式。因此,作者们采用了过程依赖的屈服函数,将当前模型扩展到了有限塑性情形。该模型允许通过减少弹性储能的积累来模拟在流体状态下扩散的材料,该能量积累可能导致意外的和非物理的弹跳行为。对于数值模拟,作者们介绍并执行了一个考虑子族及相关体积加权因子的近场动力学对应公式的增强版本。除了将特定的激光建模作为体积热源外,在近场动力学的框架中还引入了所产生的热-化学-力耦合方程中的局部-非局部耦合。在模拟中,介绍了基于塑性方法在模拟流体状态下材料扩散的适用性。最后,作者们开发了用于(模拟)基于挤压印刷工艺的软件,并模拟了完整的热-化学-力耦合的AM工艺。结果表明,通过减少应用激光照射的材料扩散,可以获得更高的几何精度。该建模过程完成了虚拟植入物开发的第一步,将来有可能用于AM工艺的优化。 图:模拟AM过程的初始构型的图解,其中喷口内的粒子用蓝色表示,印版用黑色表示,喷口用淡红色表示,其余的粒子根据到喷口z方向的距离着色。 图: 3D打印材料在不同的压出速度下的最终构型以及压出材料过程的初始和最终直径的定量比较。 文六: https://doi.org/10.1016/j.compstruct.2020.112613 用于颗粒增强金属基复合材料断裂模拟的分子动力学辅助近场动力学建模方法 本文提出了一种借助分子动力学(MD)构建界面材料本构关系的近场动力学(PD)模型,以模拟颗粒增强金属基复合材料的力学性能,并再现了和实验相似的失效模式。在数值模拟中,作者们首先提出了PD键的本构模型,并将其用于模拟Al-Al和SiC-SiC系统。然后,进行MD模拟以表征Al-SiC界面(键),并通过与现有的研究结果进行比较,验证了预测结果的有效性。之后,作者们将借助MD所构建的界面键的本构模型应用于PD模拟。通过考虑或不考虑SiC夹杂物对Al基体强化作用的两个准静态模拟,本文对更新后的PD模型的进行了验证。另外,所提出的模型还成功地预测了整个复合材料系统的失效行为。所得结果表明,本文构造的方法可成功应用于准静态问题和动态问题的研究。 图:低速冲击测试示意图。 图:近场动力学(a)和有限元(b)模拟结果比较,上下图均描述了原始的全局模型,颗粒体积分数为20%,冲击速度为3m/s,陶瓷颗粒为灰色,基体根据等效塑性应变进行着色。 图:颗粒体积分数为20%的Al-SiC样品在不同冲击速度下的局部细节,(a) 1m/s, (b) 2m/s, (c) 3m/s, 材料点根据损伤参数φ_d进行着色。 ————————————————————————————————————————————— 近场动力学(PD)理论是国际上刚兴起的基于非局部作用思想建立的一整套力学理论体系,用空间积分方程代替偏微分方程用以描述物质的受力情况,从而避免了传统连续力学中的微分计算在遇到不连续问题时的奇异性,所以特别适用于模拟材料自发地断裂过程。然而,因为近场动力学的数学理论内容丰富且与传统理论差别较大,目前的相关文献又以英文表述为主,所以很多朋友在一开始学习时会遇到一些困难。因此,我于2016年9月建立了此微信公众号(近场动力学讨论班),希望通过自己的学习加上文献翻译和整理,降低新手学习近场动力学理论的入门门槛,分享国际上近场动力学的研究进展,从而聚集对近场动力学理论感兴趣的华人朋友,为推动近场动力学理论的发展做一点儿贡献! 每期文章评述的首发平台是微信公众号:近场动力学PD讨论班 或扫如下二维码加入公众号:

图:本文中的材料模型。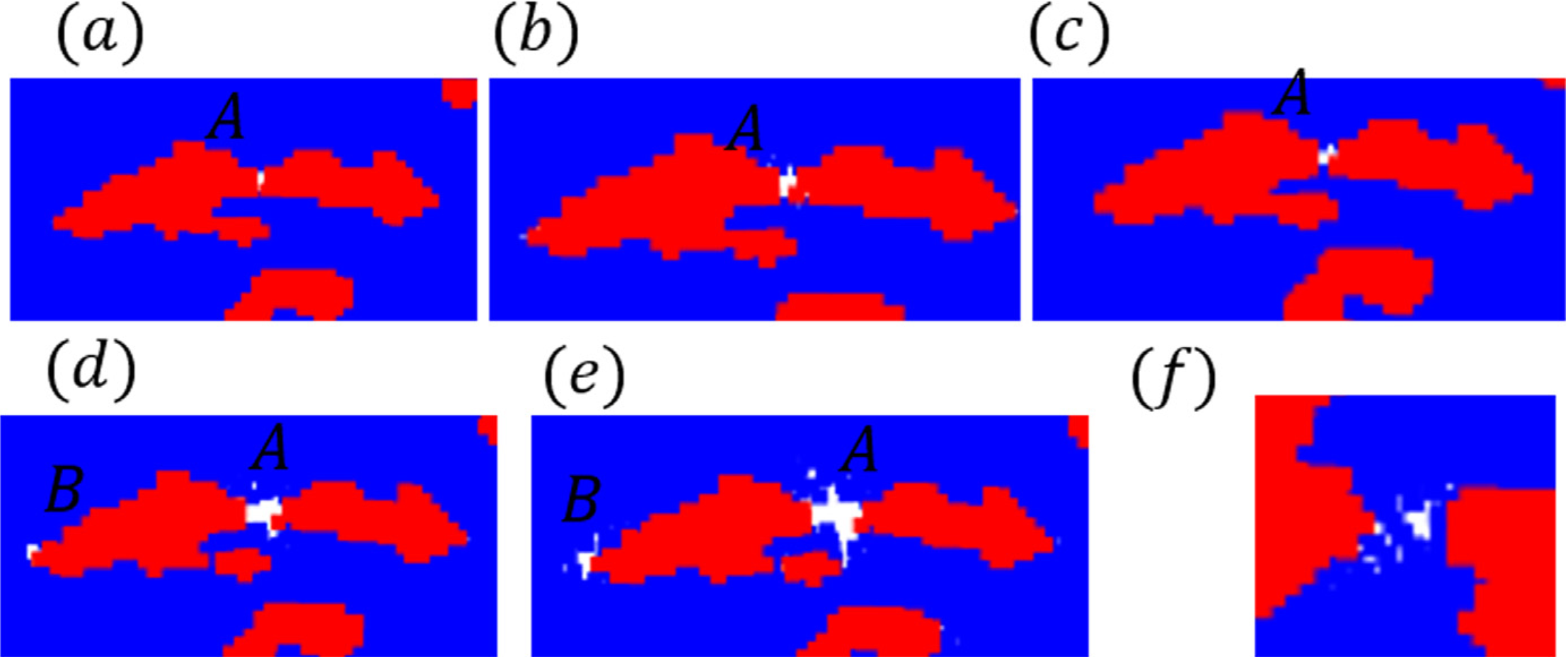



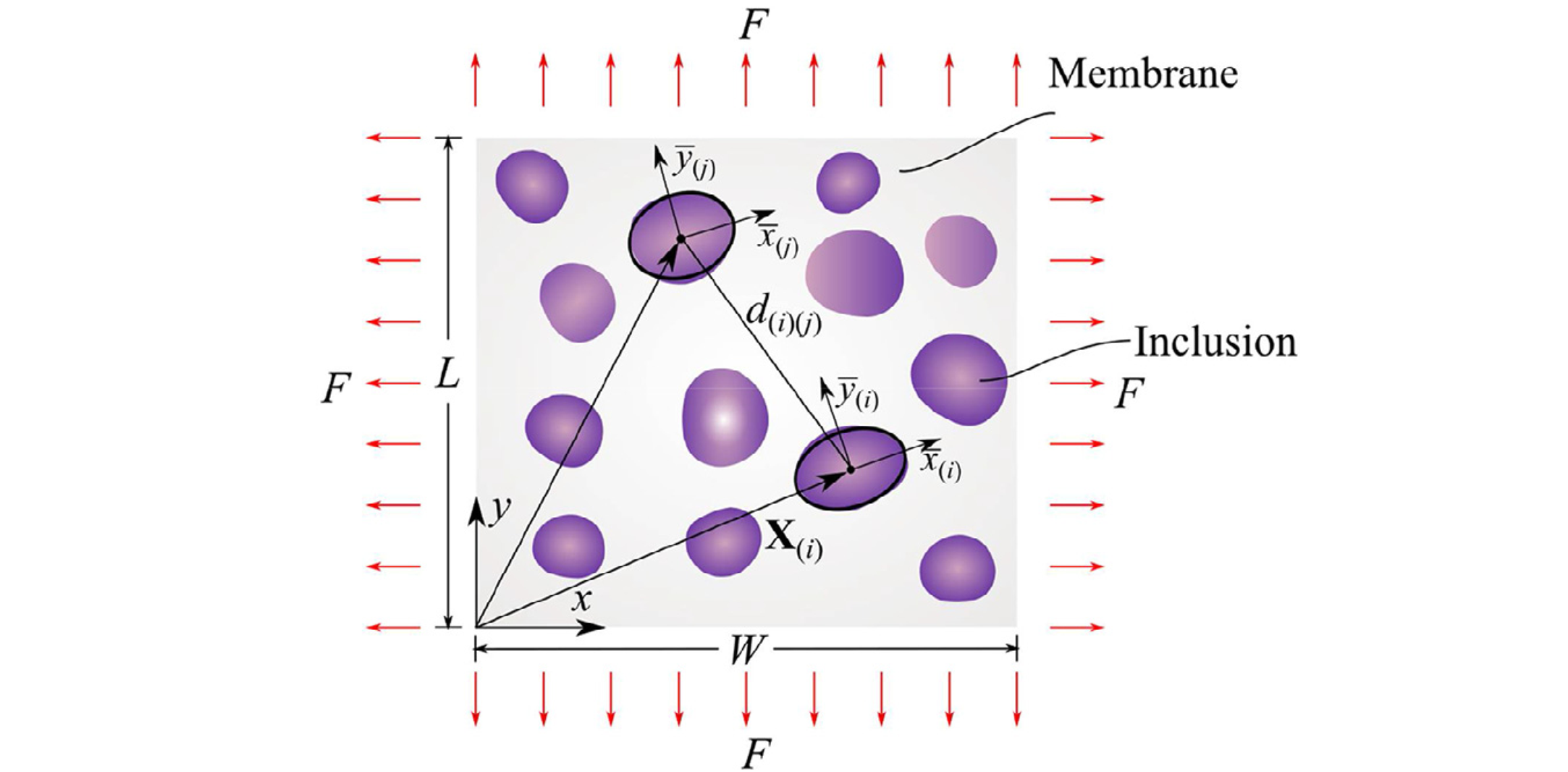
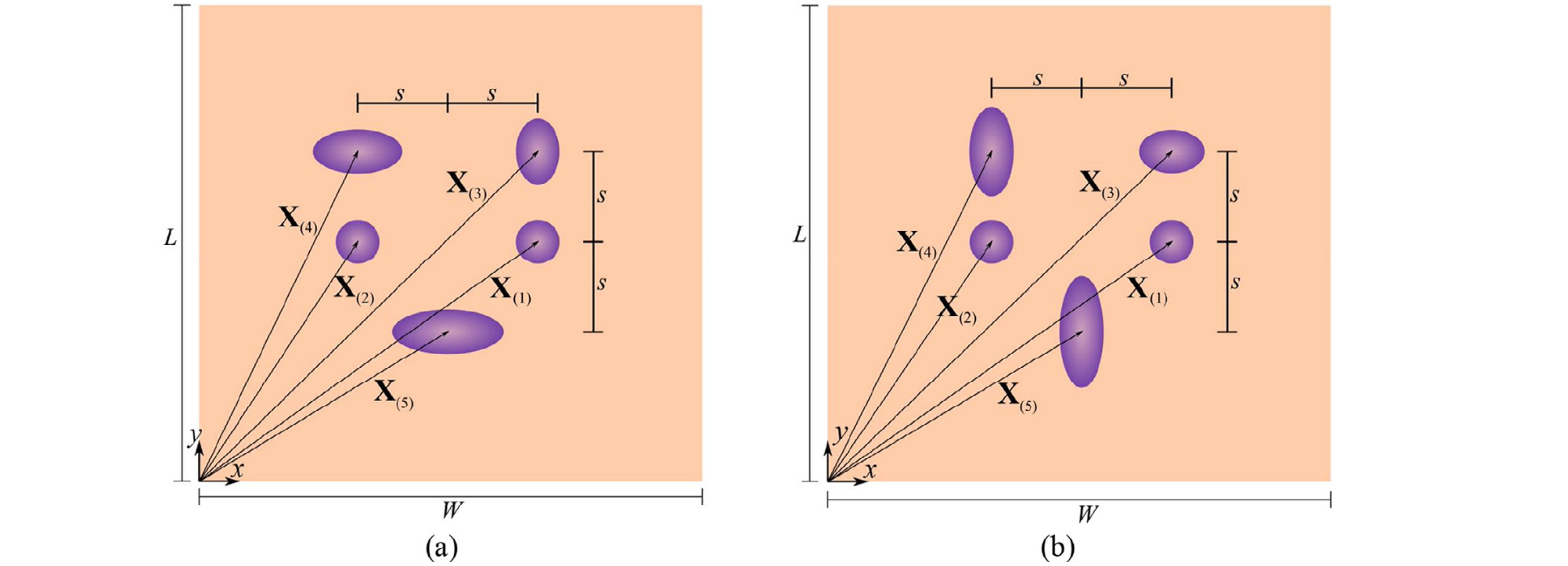
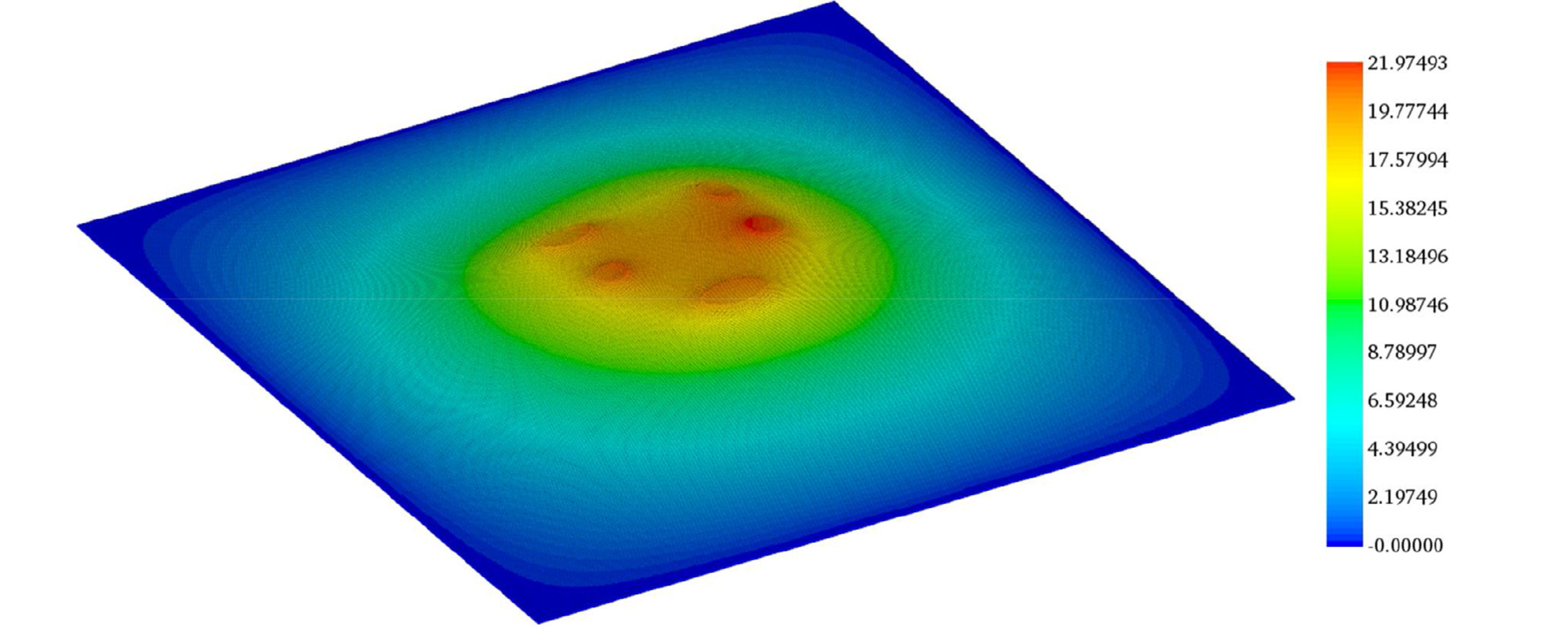

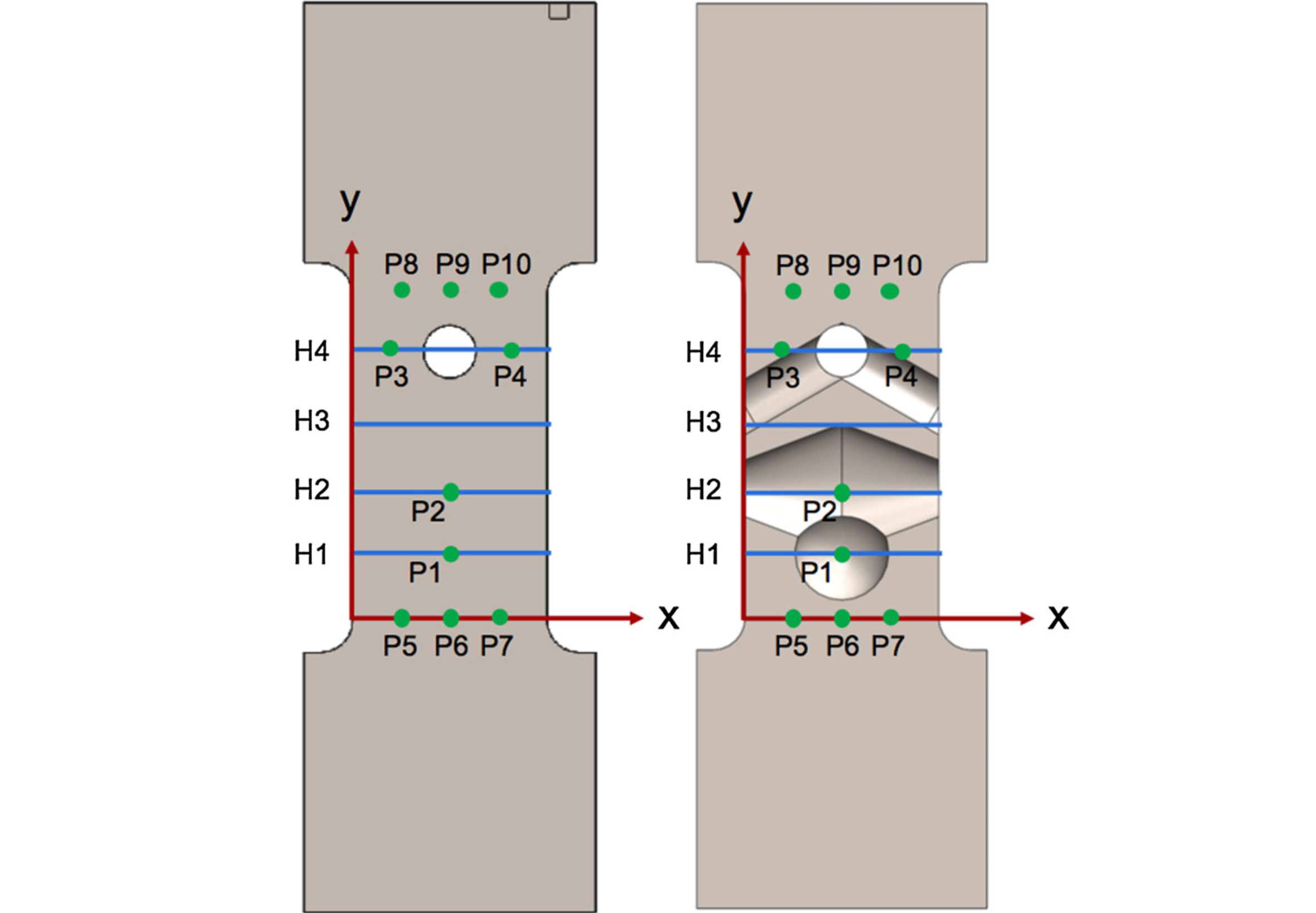

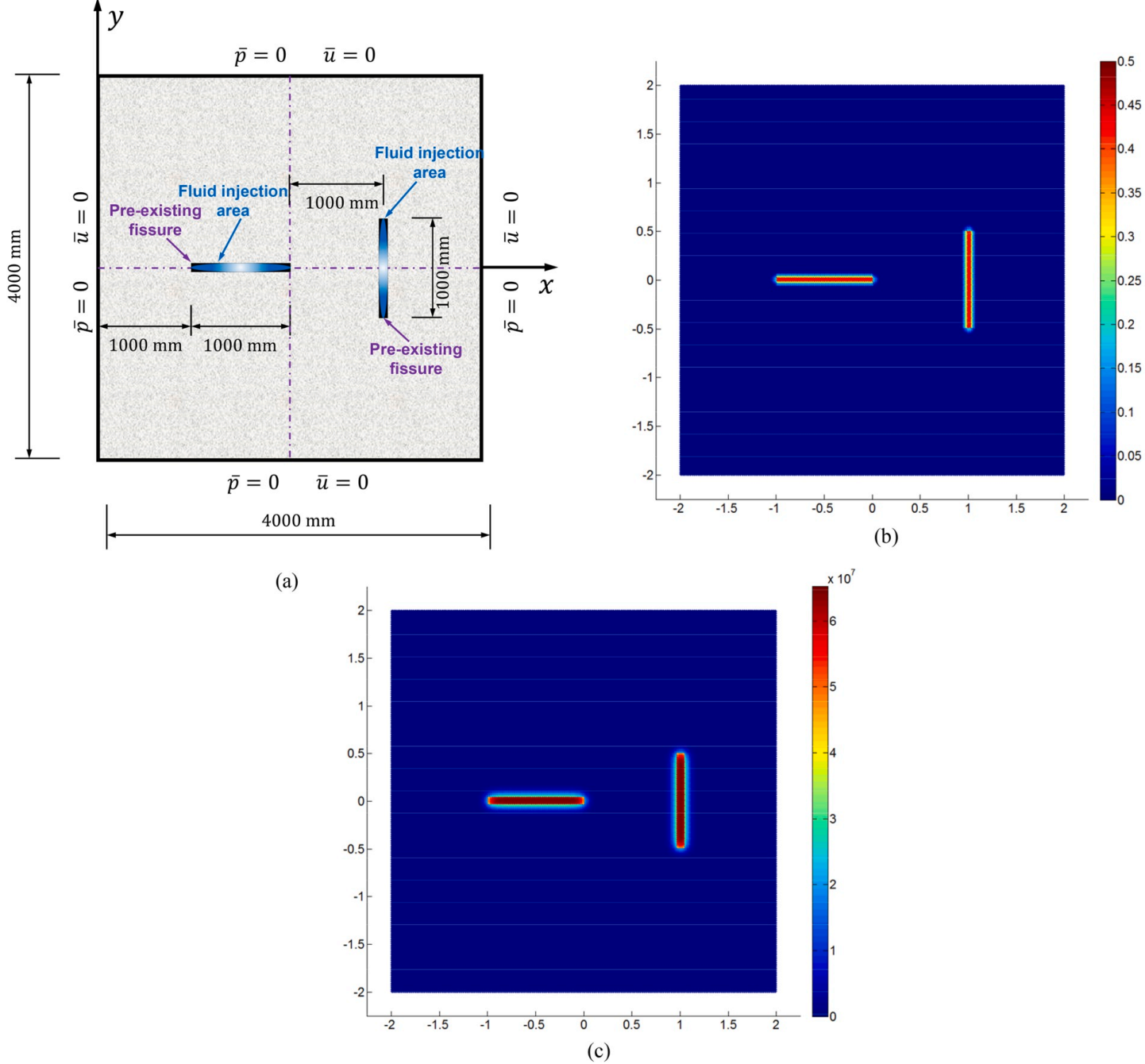


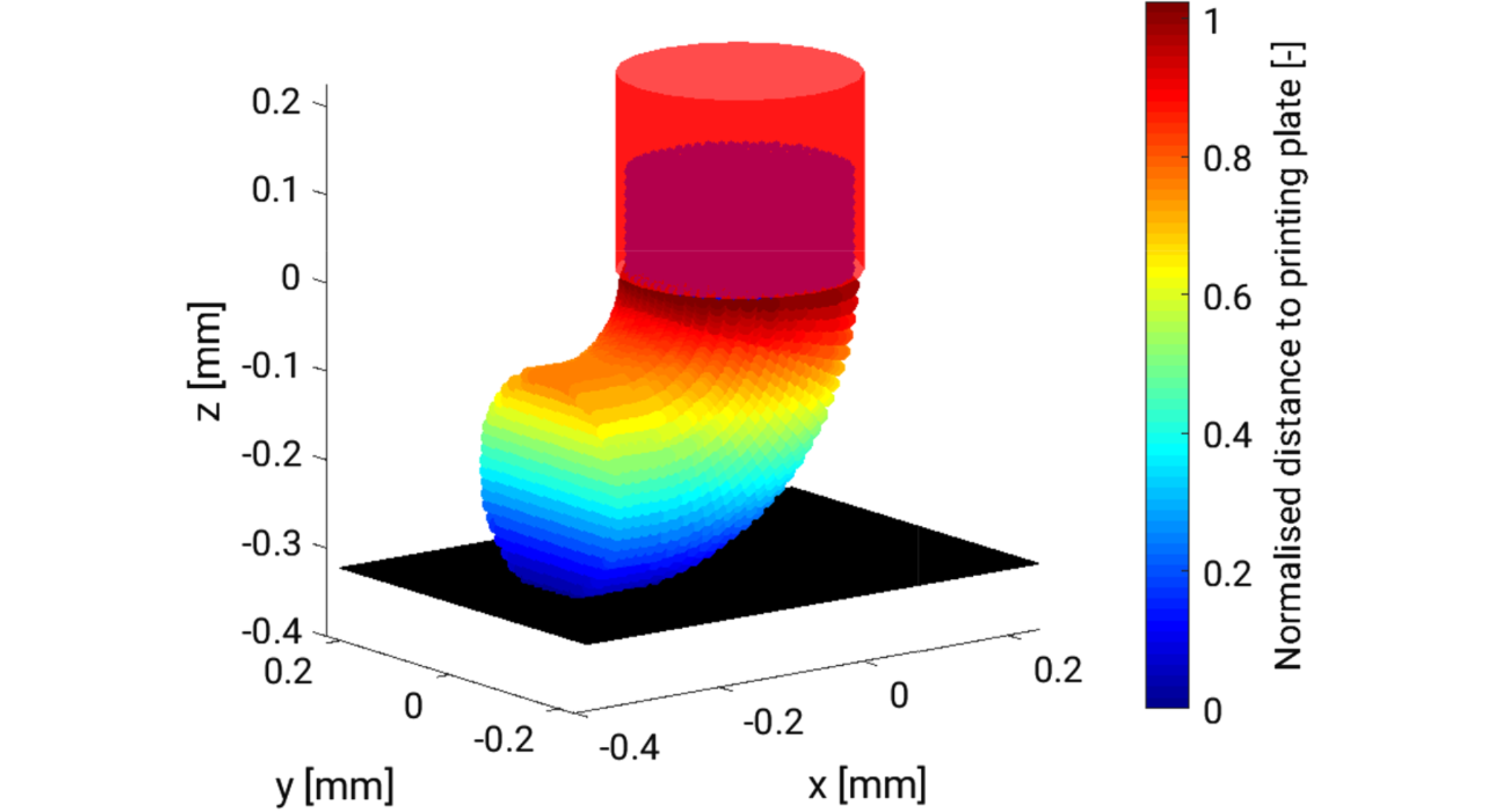


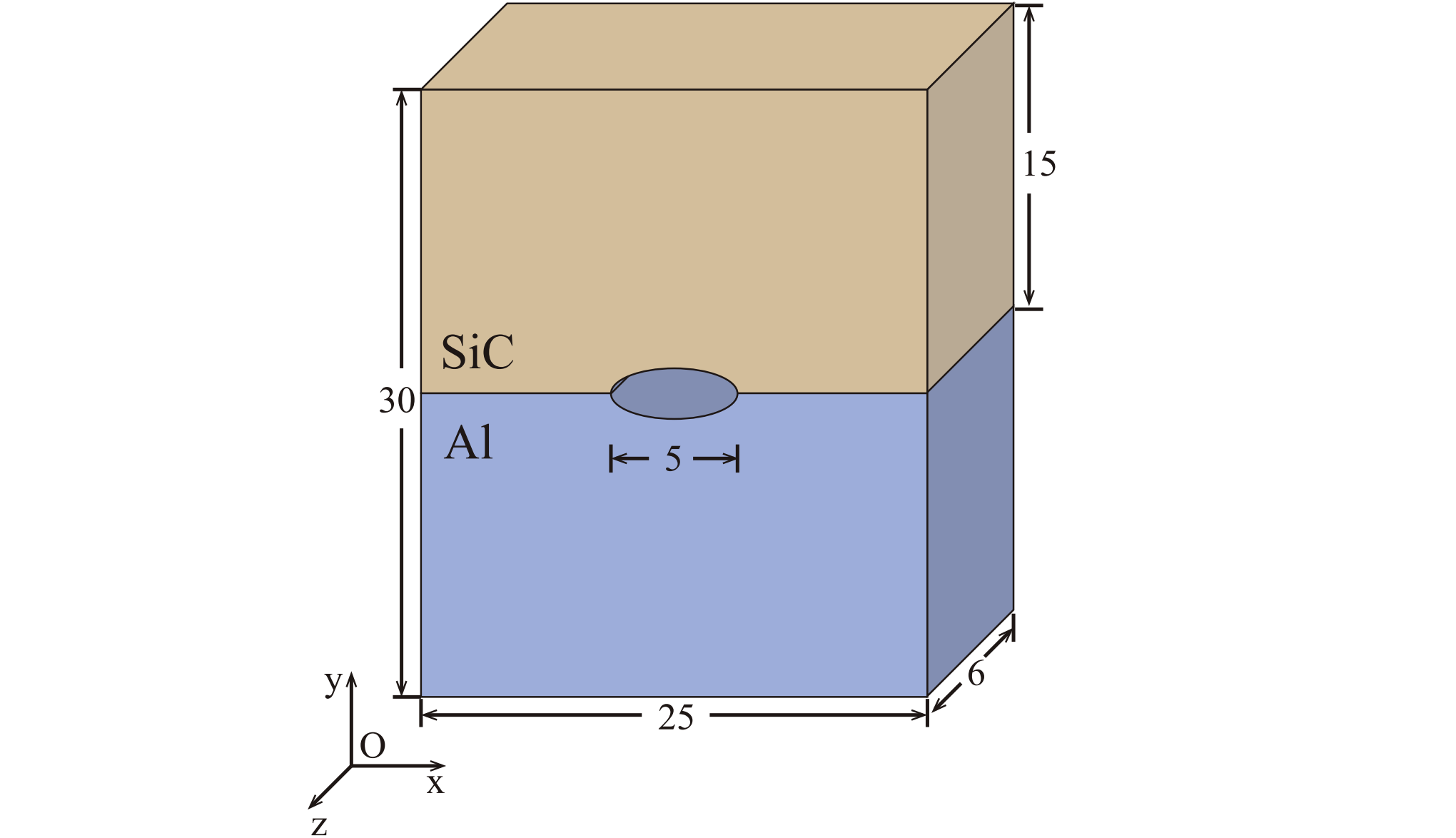
图:预置裂纹的MD模型示意图,所有的尺寸都以纳米为单位。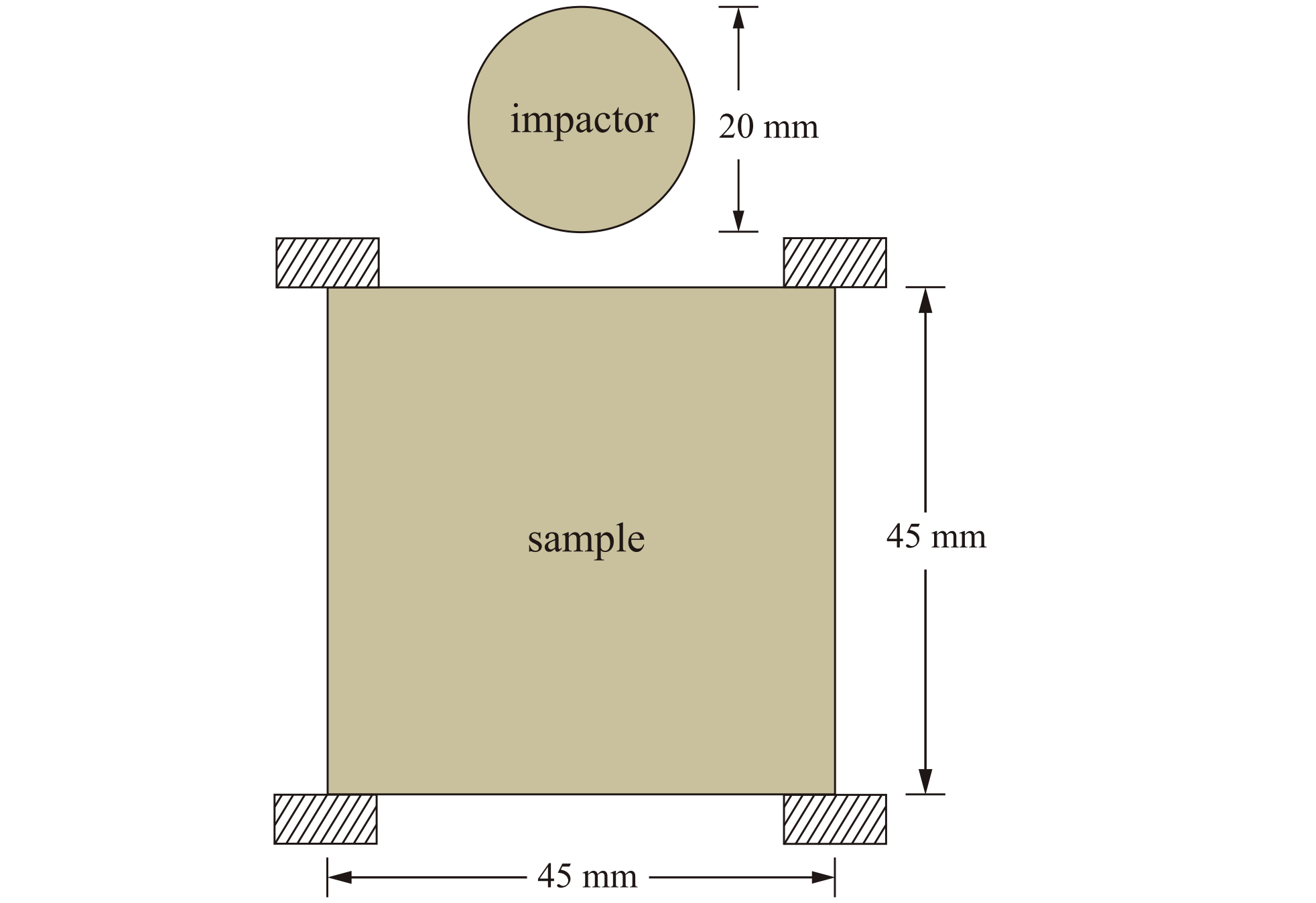

也可以搜索微信号:peridynamics
https://blog.sciencenet.cn/blog-232936-1260591.html
上一篇:近场动力学最新上线的文章快报:2020年5月(四)
下一篇:近场动力学最新上线的文章快报:2020年6月(下)