每期文章评述的首发平台是微信公众号：近场动力学PD讨论班，也可以搜索微信号：peridynamics，或扫描文末的二维码加入。

2020年4月上期近场动力学领域有五篇新文章上线。本期的文章都是将各种近场动力学模型，如微极模型、扩展模型等，应用于结构及其材料的损伤和断裂模拟中。特别是文四，发表在计算力学旗舰期刊CMAME上，提出了电力耦合的微极近场动力学模型。该模型将来有望应用于电测量技术进行结构健康监测的结构损伤评估中，感兴趣的近友们可以继续关注。下面我们依次简要介绍相关文章：

文一：

http://cdmd.cnki.com.cn/Article/CDMD-10217-1019137305.htm

基于近场动力学的舰船复合材料结构冲击损伤研究

先进的复合材料由于重量轻、比强度和比刚度大、抗冲击性好逐渐成为船舶材料的新选择。但是复合材料的各向异性特征使得其损伤形式较传统的各向同性的金属材料更为复杂，因此如何对复合材料结构的损伤断裂行为进行准确的分析和预测一直是工程和学术领域的难题。目前常用的经典连续介质力学方法在解决损伤断裂问题时在位移场不连续位置存在奇异性,而新兴的近场动力学方法，在本构模型中采用积分形式代替了传统经典力学的微分形式，且其本构模型已包含了损伤定义方法，因此采用该方法能够很好的模拟复合材料结构在破片冲击作用下和冲击波载荷作用下的损伤情况。

本文首先对近场动力学方法的历史发展过程和研究现状进行了梳理，着重介绍了该方法在冲击领域的应用和发展现状。随后对近场动力学方法的运动方程、变形函数和边界约束条件进行了详细的推导，并在此基础上介绍了适合于复合材料分析的“键”基近场动力学模型。基于“键”的近场动力学模型，编写了复合材料单层板、层合板和加筋板的冲击计算程序，并通过算例将其弹性阶段的响应与有限元计算结果进行对比，并将部分损伤结果与实验结果进行对比，验证了程序的有效性。

最后采用上述的方法分析了用于舰船防护的复合材料层合板和加筋板结构在高速破片冲击下的损伤破坏模式以及破片穿透结构后的剩余速度情况，并且综合考虑了破片的速度和几何形状、层合板的铺层方式、加筋板的筋条尺寸和破片相对筋条的冲击位置对于结构的损伤模式和破片剩余速度的影响。随后，分析了水下爆炸冲击波载荷作用下的复合材料层合板和加筋板结构的损伤及变形情况，考虑了爆炸冲击因子、纤维性能与铺层方式、筋条尺寸以及分布距离对冲击波作用下的复合材料结构的损伤及变形情况的影响。通过上述模拟分析给出一些具有工程实际意义的结论。

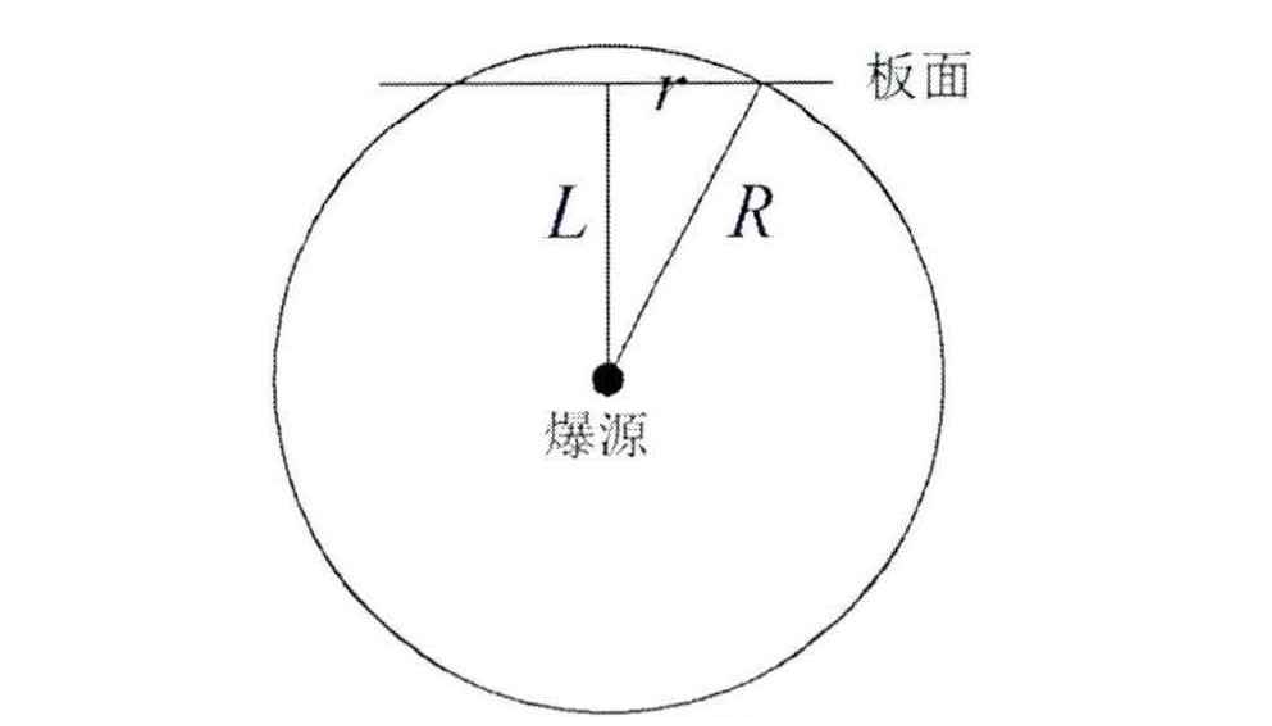
图：冲击波作用范围示意图。

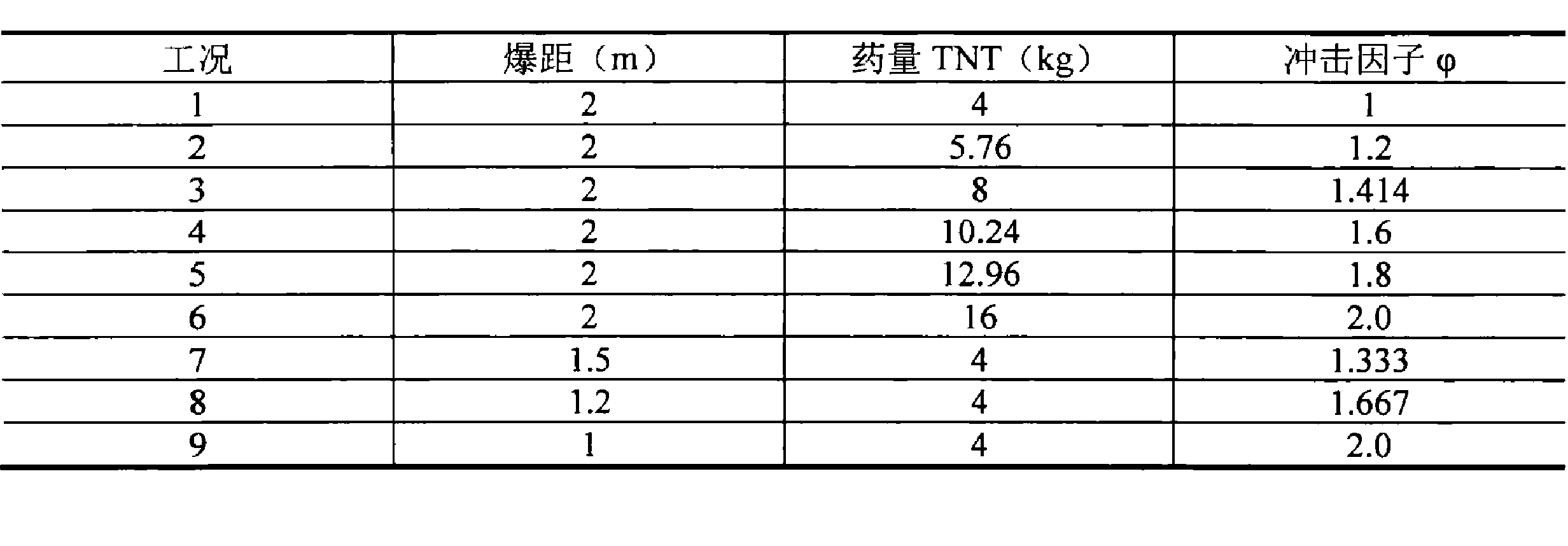
图：不同的爆炸计算工况。

图：不同工况下的层合板损伤情况。

文二：

https://works.bepress.com/javad-mehrmashhadi/4

模拟受微结构和温度影响的动态与准静态脆性断裂的近场动力学模型

数值模拟作为理论和实验分析之外的另一种方式被大量研究，用以理解脆性破坏。本文正是采用近场动力学模型研究了动态和准静态脆性断裂。

材料的失效始于微观尺度并且有时会灾难性的影响到结构的尺度。对断裂进行计算建模的目标是为了预测裂纹/损伤的萌生、生长与合并。实现了这一目标就能指导设计人员改变材料的微观结构设计，以增加韧性和可靠性。作者首先介绍了焊点的微结构层次近场动力学模型，以了解动态加载条件（跌落试验）下的断裂演化。荷载由更大尺度传递来，为此作者们建立了板层次的有限元分析。结果表明，含有较大夹杂物的试样比含有较小夹杂物的试样有明显较多的裂纹，这与实验观察结果吻合较好。

上述方法（材料微尺度的显式表征）对于具有相对较大的损伤区域的问题计算上变得非常困难，如纤维增强复合材料（FRC）。模拟FRCs线性弹性行为的均匀化方法已经很好的建立了，但不能用于断裂，非线性和耗散现象。本文中，作者们（用Halpin-Tsai均匀化方法）建立了一个完全均匀化的近场动力学（FH-PD）模型，用于模拟单项FRCs的横向断裂。作者们展示了该模型的一些局限性，并为单向FRCs的横向荷载引入了一种新的半均匀化的近场动力学（IH-PD）模型。作者们表明，IH-PD模型导致裂缝路径的曲折度类似于实验观察到的曲折度，并且不需要FRCs微观结构的明确表示。

几十年来，对于PMMA材料动态裂纹扩展过程中所测得的裂纹扩展速度，计算模型一直存在着过度预测的问题。实验表明，PMMA在断裂过程区产生高温，使裂纹尖端周围的材料软化。作者们通过引入一个新的本构模型来考虑这一影响：靠近裂纹尖端的近场动力学键明显比其他材料的键要软。新模型计算的裂纹扩展速度和裂纹扩展长度与实验结果吻合较好。

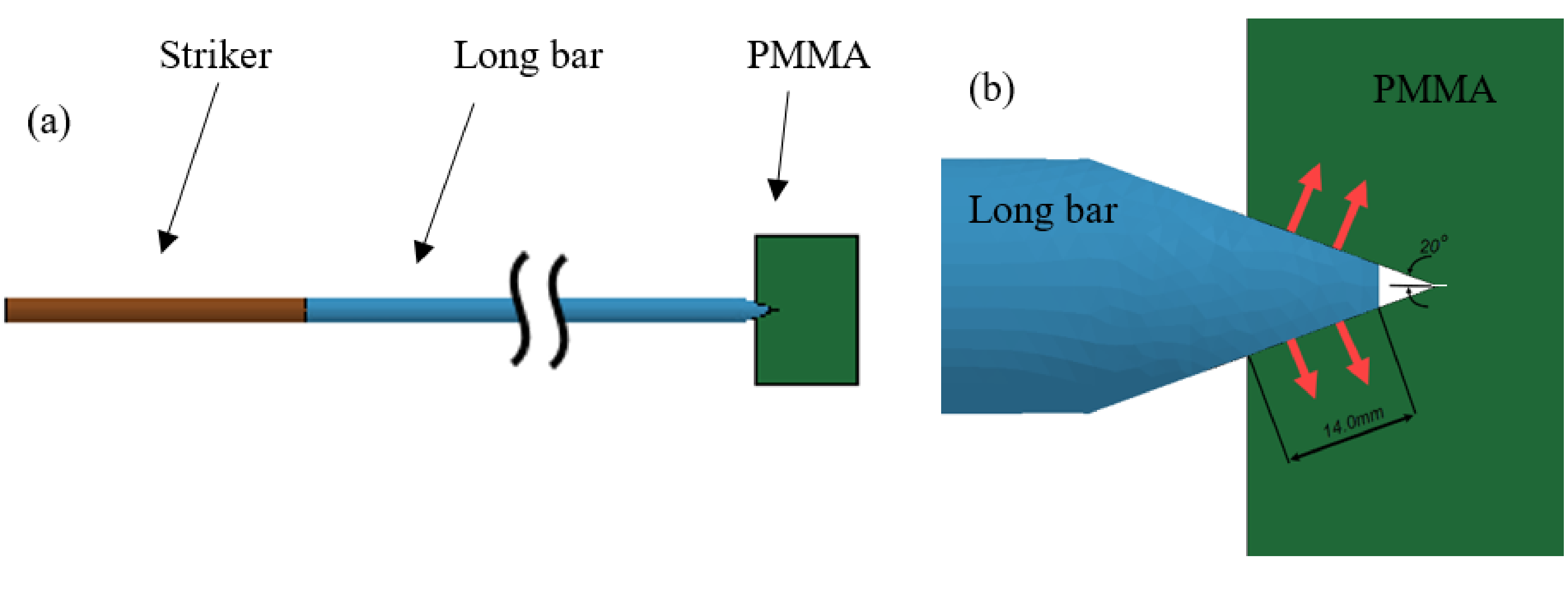
图：(a) LS-DYNA FE模型的几何设置，(b) 冲击长杆与带有v型缺口的PMMA试样之间的相互作用。

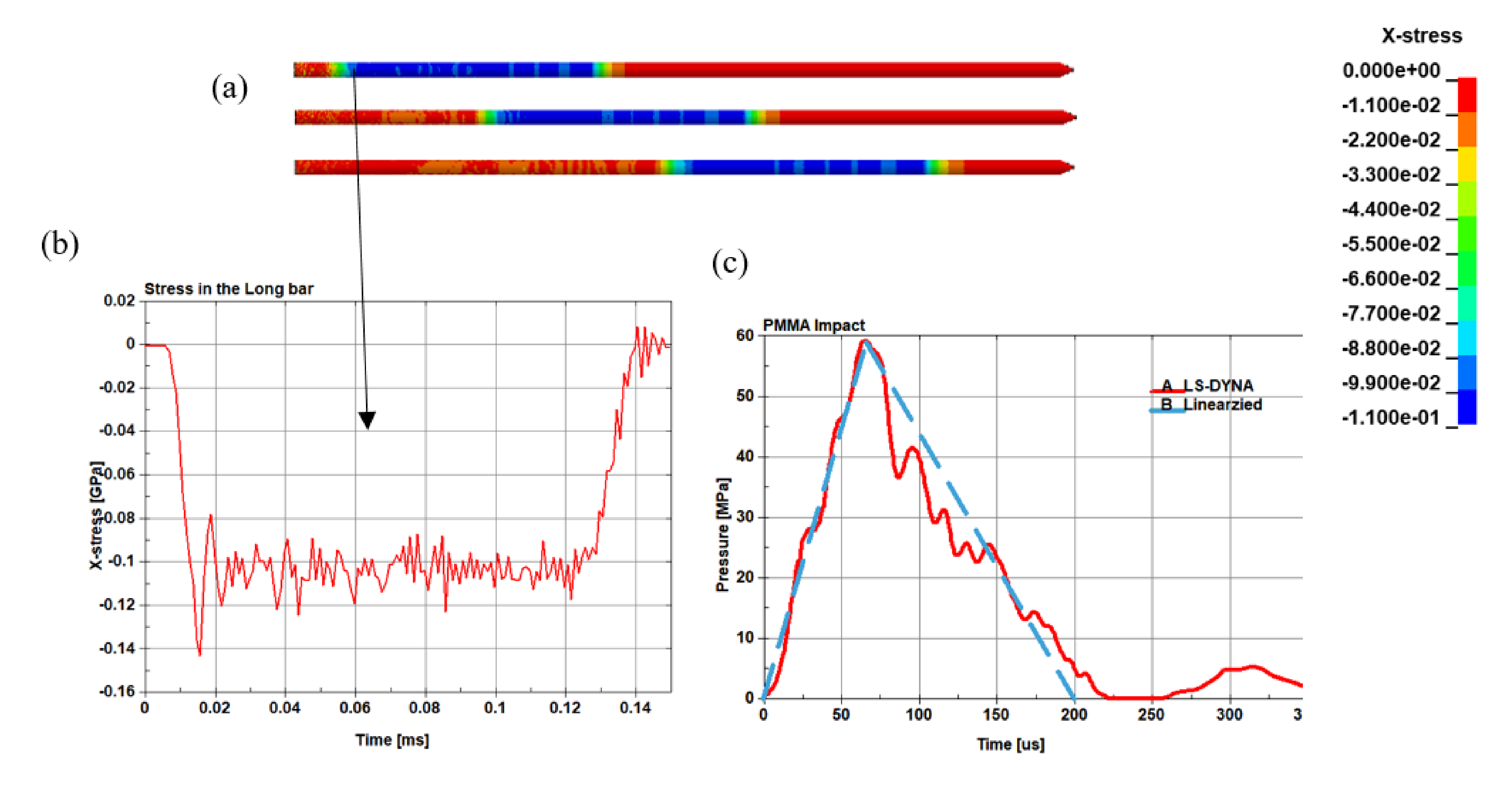
图：(a)长杆内的压应力波，(b)长杆内压应力波的传播，(c) v型缺口表面的压力测量。

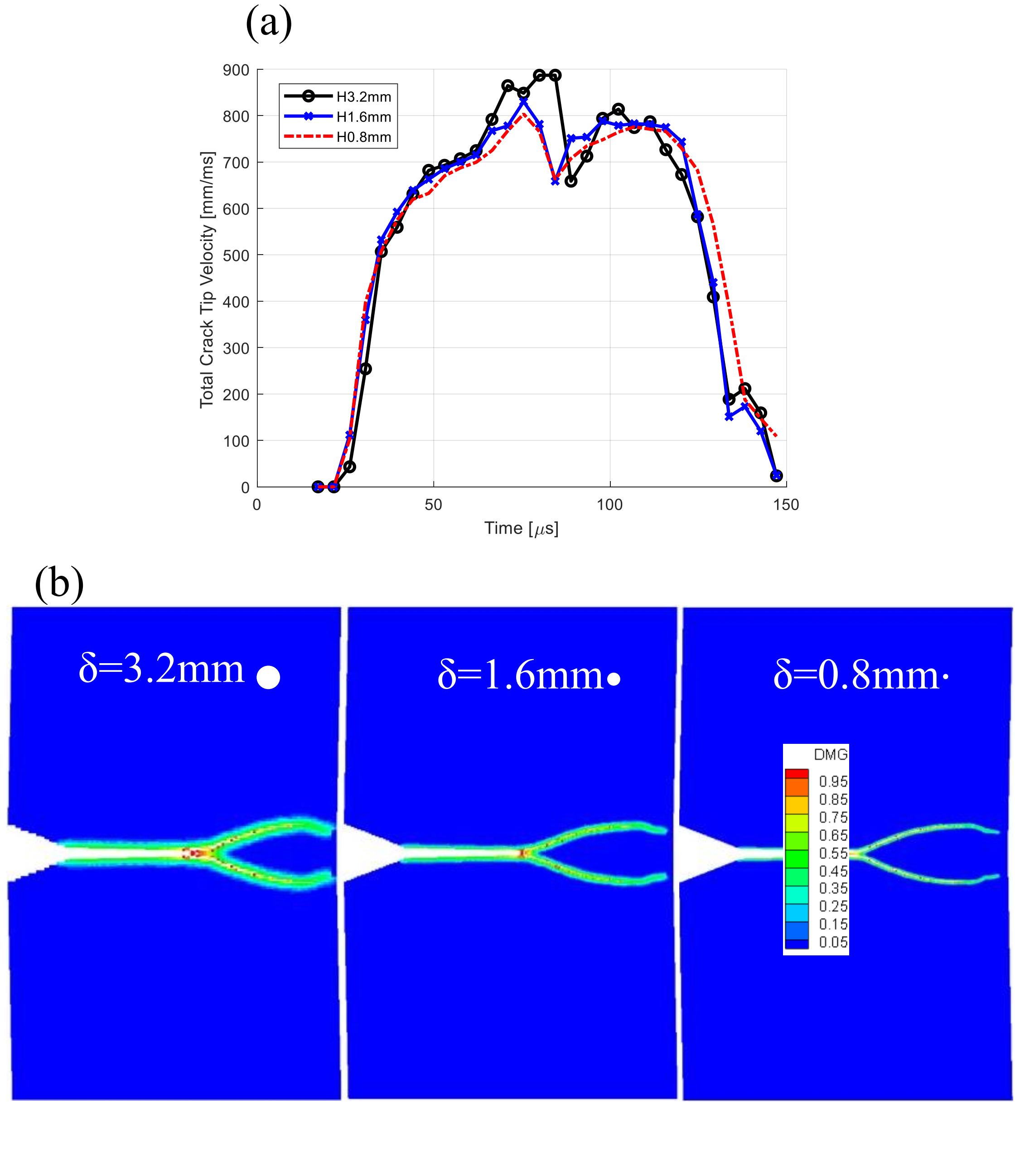
图：影响域分别为δ=3.2，1.6，0.8mm的单片PMMA近场动力学模型的收敛性研究；(a) 开裂速度变化历程，(b) 模拟结束时的变形形态，（颜色表示损伤分布，小的白色圆盘表示使用的每个影响域的相对大小）。

文三：

https://doi.org/10.1016/j.ijsolstr.2020.03.025

各项同性和正交各向异性的微极近场动力学固体中的裂纹弯折

本文提出了一种微极近场动力学模型，以表征各向同性和正交各向异性材料中脆性材料的裂纹扩展。二维模型的解析式基于微势能函数的定义，该函数考虑了定义正交各向异性的四个独立弹性常数，并且在极限情况下可以将其简化为各向同性。该模型的一个显著特征是键的弹性参数是沿材料的主轴方向的连续函数。通过定义量化键伸长、键的剪切变形和粒子的相对转动三个变形参量，作者们获得了第一个连续的键型近场动力学模型并应用于以四个独立材料模量表征的二维柯西正交各向异性材料。该模型适合于描述断裂以及均匀变形和非均匀变形。

本文通过将紧邻裂纹的边界层中的位移和应力场与正交各向异性连续介质的解析渐近结果进行比较，评估了计算模型应用于裂纹尖端分析的准确性。基于本文假设的裂纹扩展准则，作者们模拟了此类裂纹在混合加载条件下的扩展，并将预测结果与根据最大环向应力强度因子准则（HSIF准则）和最大能量释放率准则（G准则）的预测进行了比较。

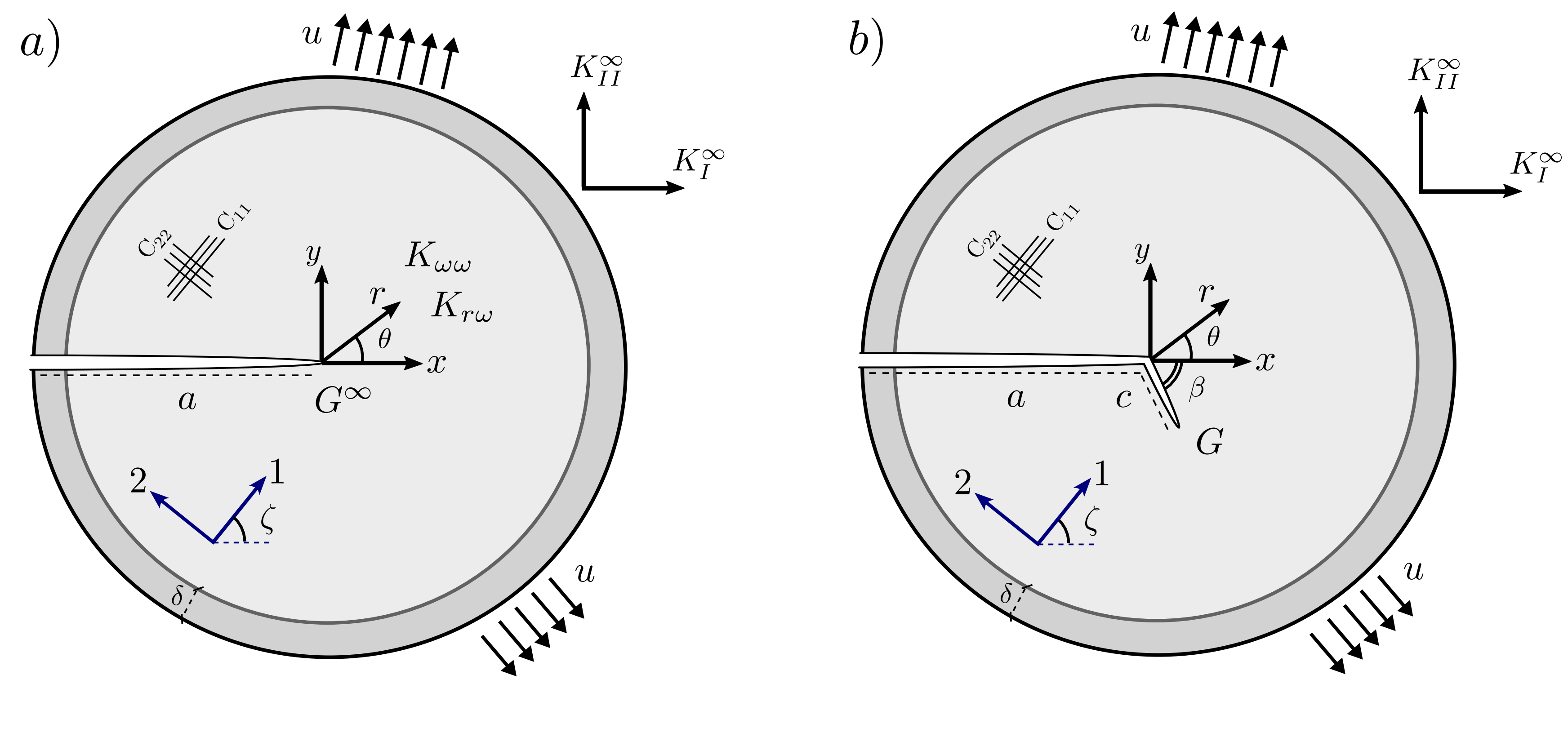
图：正交各向异性介质中近尖端解分析的几何条件和边界条件，(a)半无限裂纹; (b)弯折裂纹。

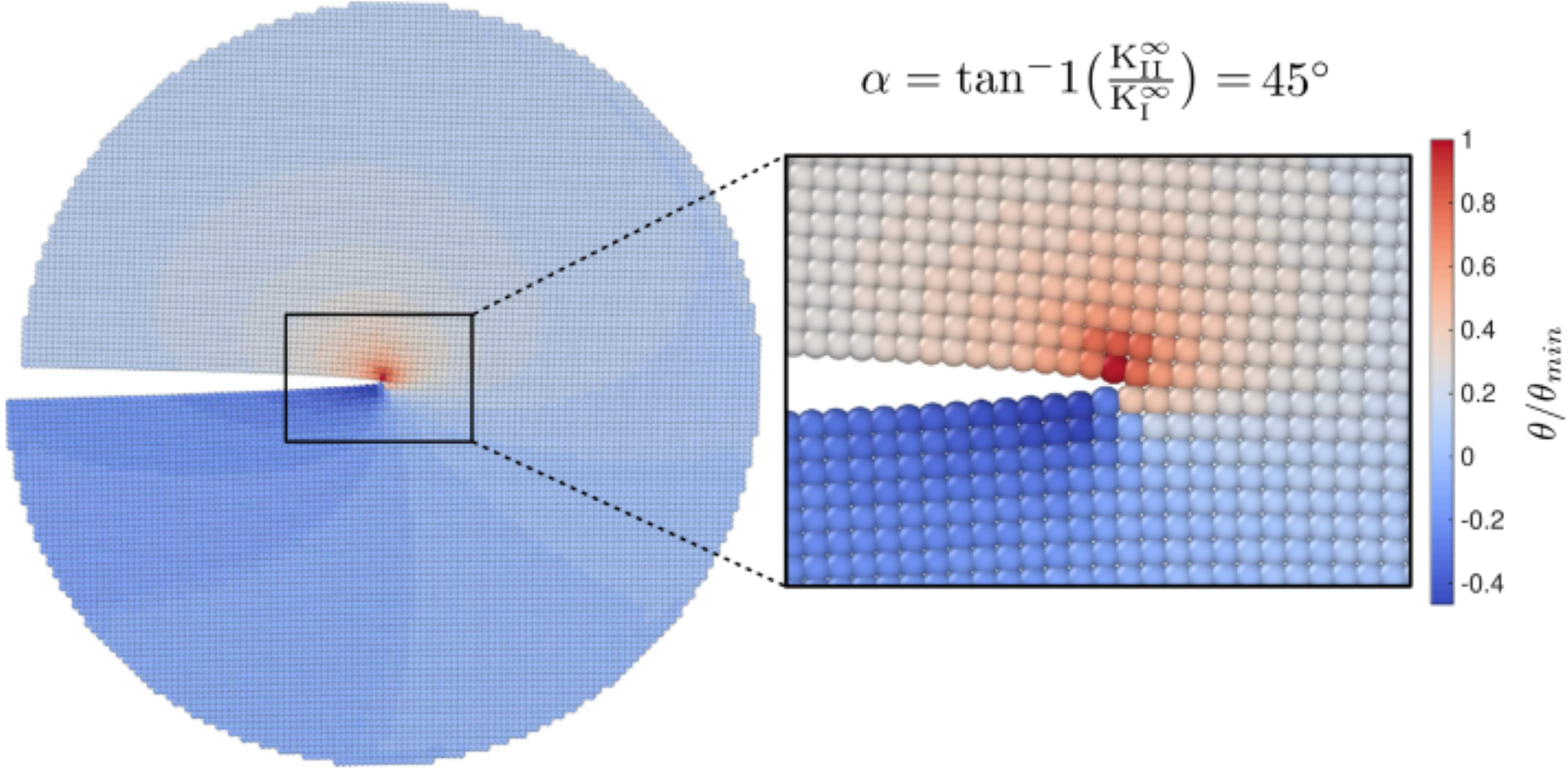
图：混合模型Ⅰ-Ⅱ（α=45°）在λ=0.2，ρ=1.1的正交各向异性材料情况下的粒子旋转图，在高应变梯度区，如裂纹尖端附近，旋转的强度更高。

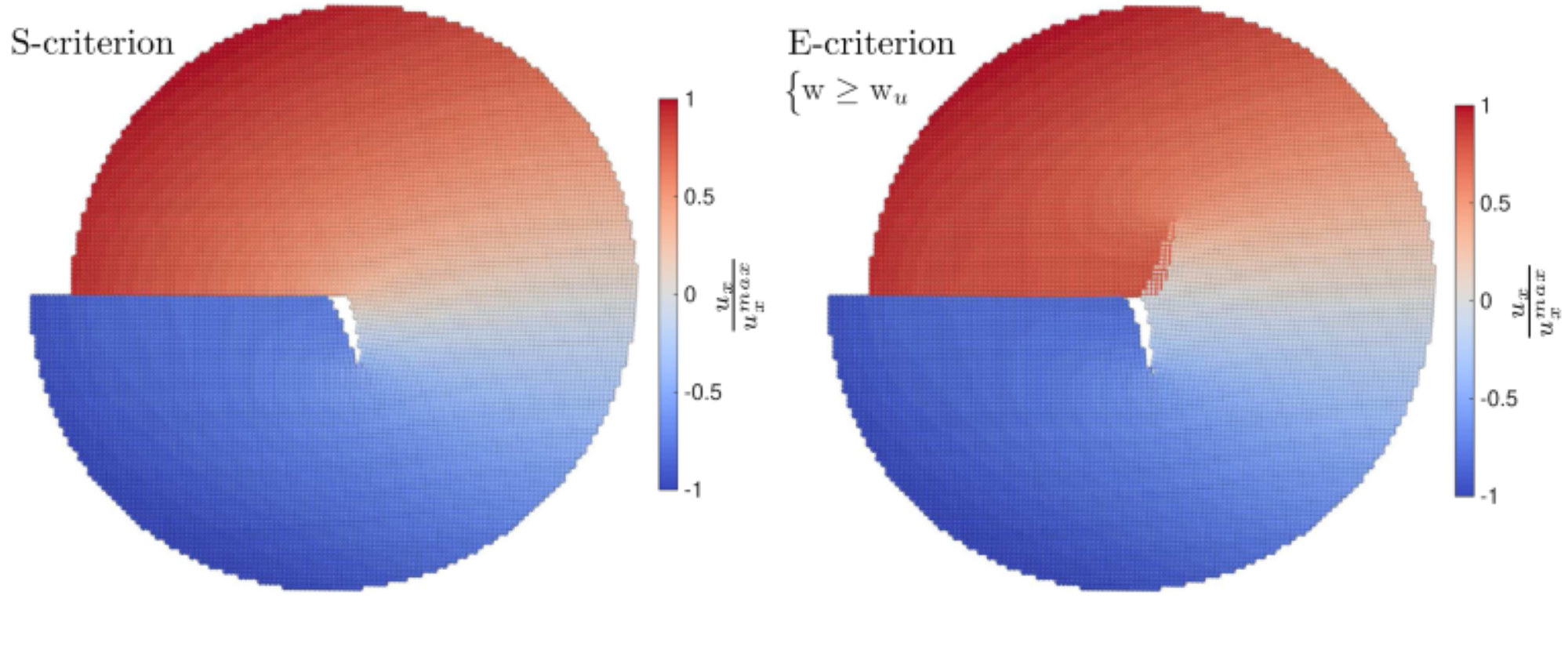
图：MAT3, 立方对称（模型Ⅱ）：根据S-准则和E-准则（无键拉伸符号条件）的扭裂，与G-准则的预测相似，根据标准E-准则，裂缝发生分叉是因为断裂准则为裂缝在两个方向上的打开提供了几乎相同的机会。负弯折角与拉应力有关，而正弯折角与压应力有关。

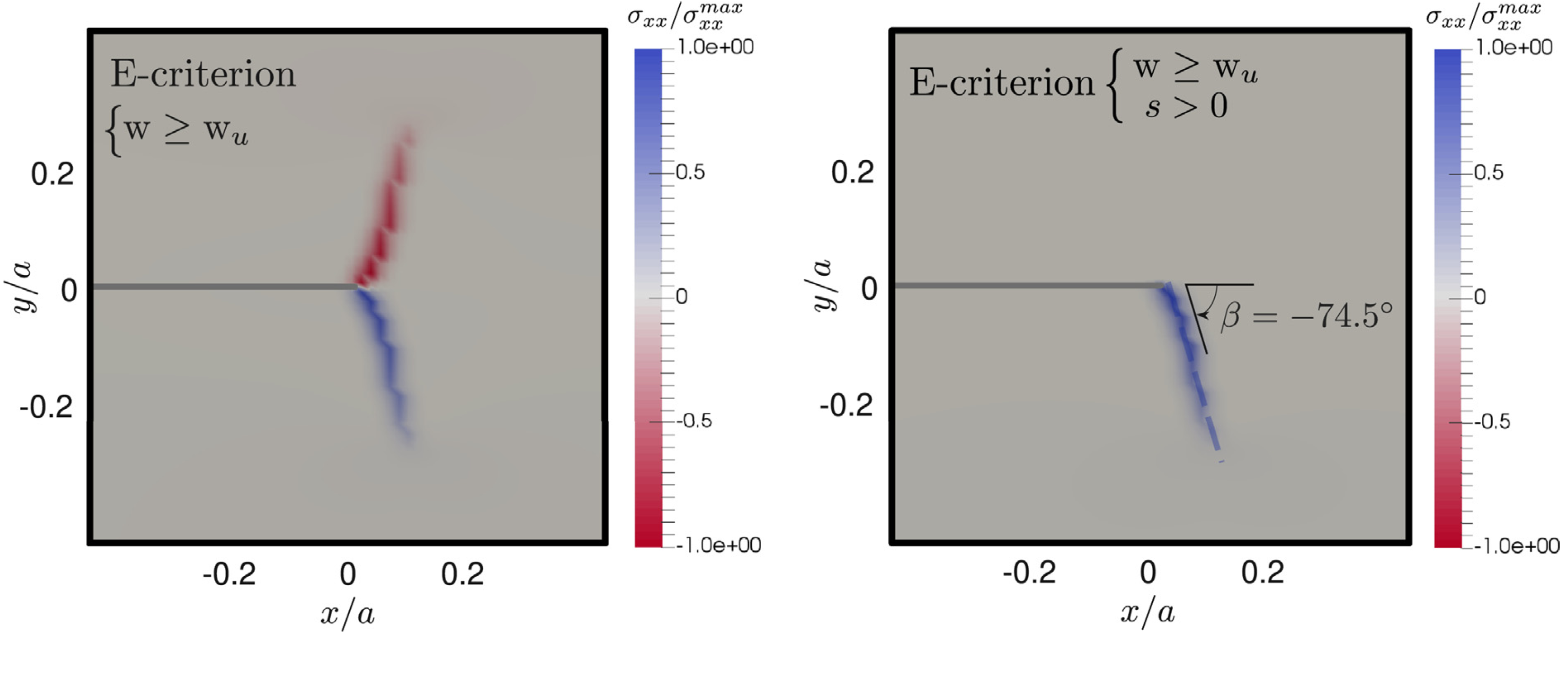
图：MAT3, 立方对称（模型Ⅱ）：分别采用标准E-准则和含有正的键拉伸条件（防止压力区裂纹扩展）的E准则预测的裂纹扭转（σ_{xx}应力图）。

文四：

https://doi.org/10.1016/j.cma.2020.112998

一个电力耦合的微极近场动力学模型

本文提出了一种用于各向同性固体的面内电力耦合行为的微极近场动力学模型。该模型电相关的隐式公式是基于一个微电能函数和特定的键电场测度所定义的。本文得出了相容性条件和本构关系，从而获得了电刚度算子。然后将电学公式和含有可调泊松比的力学微极近场动力学公式相耦合。考虑到裂缝和其他缺陷的影响，本文所获得的统一模型能够预测脆弹性材料的弹性响应和导电性。作者们通过几个问题对所提出模型的准确性进行了评估，其中包括在拉伸载荷下模拟板中的裂纹扩展和损伤感测以及纳米复合材料的力阻响应。

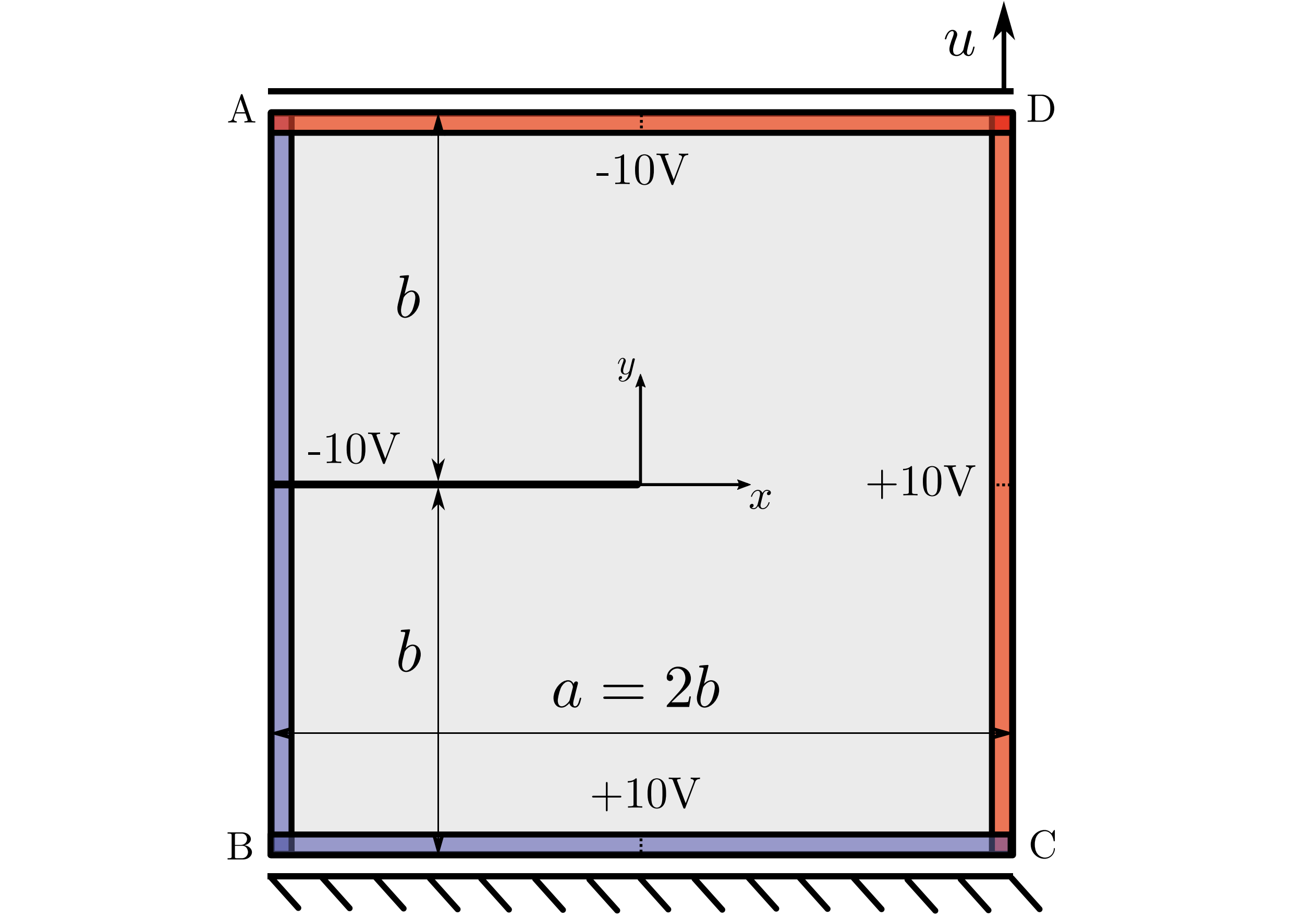
图：单边切口试样的拉伸试验：用于损伤检测的力和电边界条件。

图：单边切口试样的拉伸试验：损伤图和ΔΦ(AB-DC)，ΔΦ(AD-BC)产生的电势场，(a) u=6.98x10^{-3}mm, (b) u=7.04 x10^{-3}mm, (c) u=7.08 x10^{-3}mm。

文五：

https://doi.org/10.1155/2020/9568015

分析脆性材料断裂的扩展键型近场动力学方法

为了提高键型近场动力学的计算精度，本文引入了一种新的衰减函数来描述内长尺度对非局部作用力的影响。此外，推导了微模量函数的表达式，并建立了相应的断裂准则，并通过三个数值算例说明了扩展键型近场动力学模型的有效性和精确性。这三个数值算例分别是：单轴载荷下的二维各向同性板；准静态载荷下具有圆形切口的平板和一个中心含一条预置裂纹的对角加载方形板。最后，应用所提出的方法研究了预置裂纹的宽度和角度对裂纹萌生时间和裂纹扩展路径的影响。

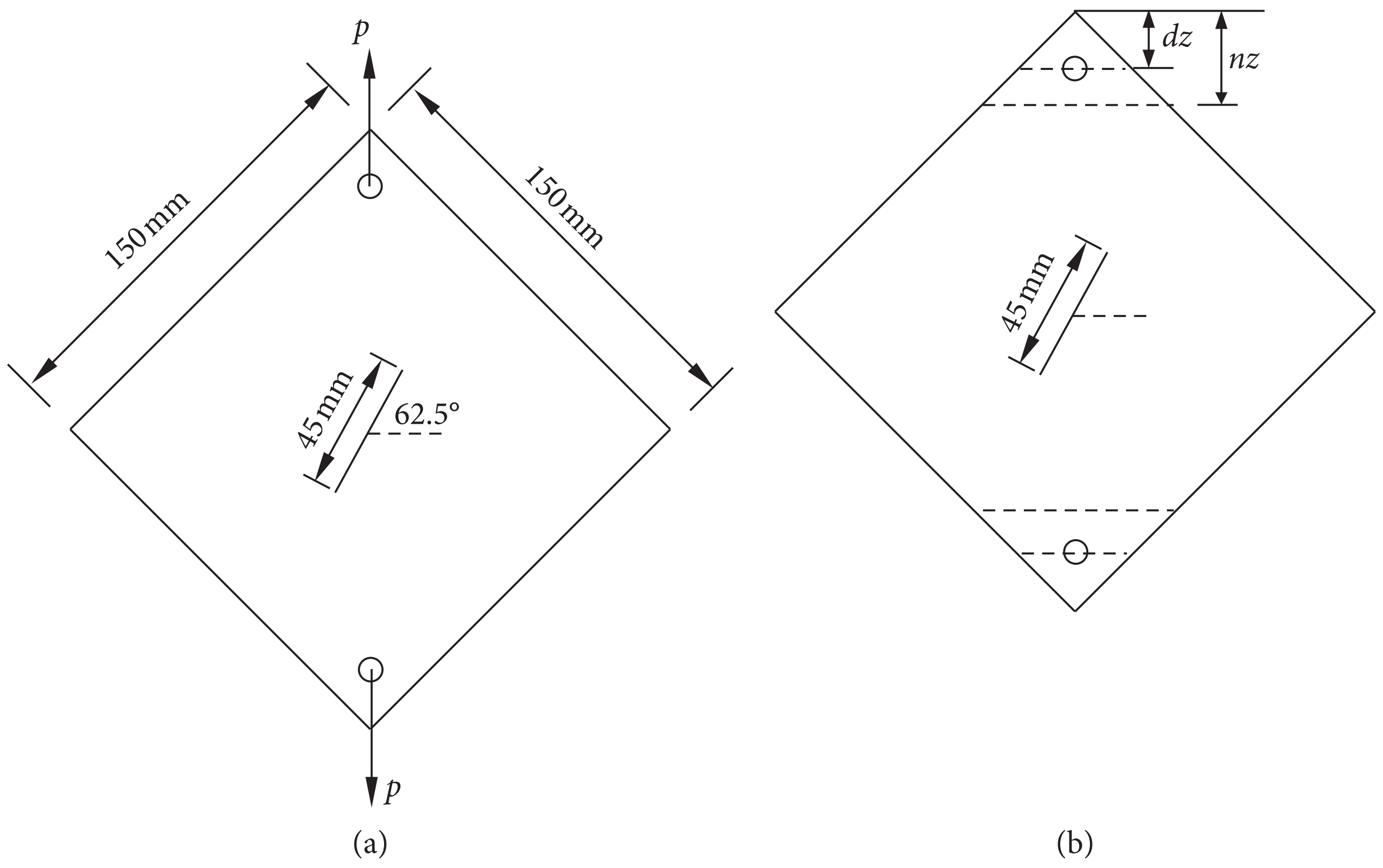
图：带有预置裂纹对角加载的二维板：(a) 实验模型，(b) 扩展键型近场动力学模型。

图：板的裂纹扩展比较，本文提出的数值模型在(a) t=25μs, (b) t=235μs, (c) t=275μs, (d) t=335μs, (e) t=422μs的模拟结果，(f) 实验结果。

图：中心裂纹板的几何参数和加载条件。

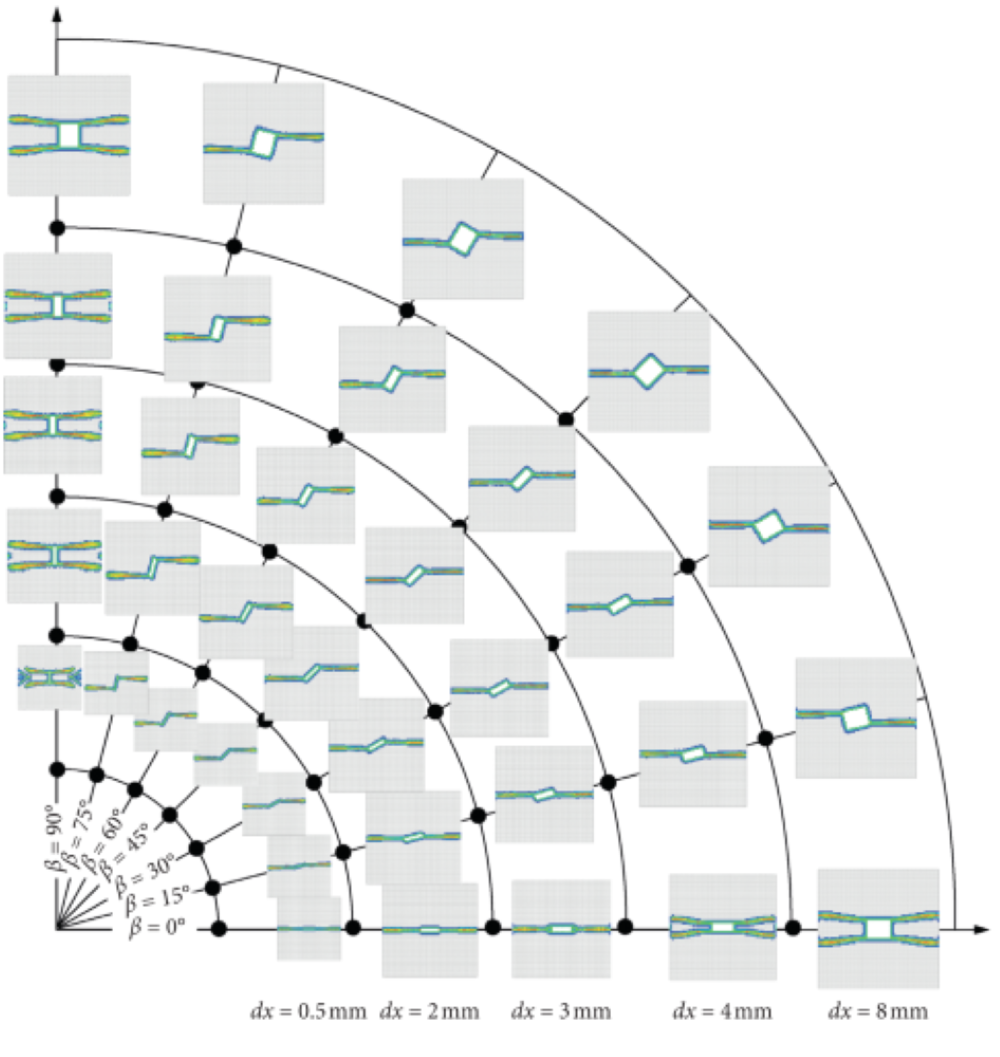
图：不同裂纹宽度dx以及不同方向角β下的裂纹扩展。

—————————————————————————————————————————————

近场动力学(PD)理论是国际上刚兴起的基于非局部作用思想建立的一整套力学理论体系，用空间积分方程代替偏微分方程用以描述物质的受力情况，从而避免了传统连续力学中的微分计算在遇到不连续问题时的奇异性，所以特别适用于模拟材料自发地断裂过程。然而，因为近场动力学的数学理论内容丰富且与传统理论差别较大，目前的相关文献又以英文表述为主，所以很多朋友在一开始学习时会遇到一些困难。因此，我于2016年9月建立了此微信公众号（近场动力学讨论班），希望通过自己的学习加上文献翻译和整理，降低新手学习近场动力学理论的入门门槛，分享国际上近场动力学的研究进展，从而聚集对近场动力学理论感兴趣的华人朋友，为推动近场动力学理论的发展做一点儿贡献！

每期文章评述的首发平台是微信公众号：近场动力学PD讨论班
也可以搜索微信号：peridynamics

或扫如下二维码加入公众号：