博文
近场动力学最新上线的文章快报:2018年4月(中)
||
每期文章评述的首发平台是微信公众号:近场动力学PD讨论班,也可以搜索微信号:peridynamics,或扫描文末的二维码加入。
2018年4月中期有五篇新文章上线。下面我按照上线的先后顺序依次简要介绍:
文一:

http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yylxxb201801019
在键型近场动力学原理、数值计算方法的基础上,作者们模拟分析了无预设裂缝二维板结构在承受准静态拉伸、压缩、剪切速度边界条件下板内裂缝的形成与扩展,也分析了有预设裂缝二维板结构在快速拉伸速度边界条件下板内裂缝的形成与扩展。结果表明,键型近场动力学在两种结构状态的不同边界条件下都能捕捉到板内裂缝复杂的发展过程,而且在模拟过程中裂纹自然扩展,能准确反映宏观材料渐进破坏过程中的细微观结构变化过程。

图:板承受不同的边界条件以及离散结构

图:在压缩(上)拉伸(中)和剪切(下)条件下的板损伤预测图
文二:

https://arxiv.org/abs/1804.00273
作者们受近场动力学模型的启发研究了一种演化方程,它具有一个奇异的成对相互作用力项。并且,作者们针对柯西问题给出了在时间上具有存在性、唯一性和稳定性的全局解。
文三:

https://doi.org/10.1016/j.jcp.2018.03.043
本文提出了一种流体力学中涉及不规则分布和不连续问题的改进粒子方法。由于在计算精度、动量守恒和控制方程可行性等方面存在问题,传统的粒子法,即本文介绍的移动粒子半隐式(Moving Particle Semi-implicit, MPS)方法不能保证计算的准确性和稳定性,而Navier-Stokes方程的散度计算在不连续的计算域中可能引起数值误差。为了提高粒子方法的计算精度,我们用一个修正的张量来改进梯度算子,该修正张量能通过最小化一阶泰勒展开式的局部误差得到。另外,在近场动力学(该方法通常用于固体力学领域)的启发下,作者们提出了一种新的满足动量守恒的积分型控制方程。通过将改进的梯度算子和新型控制方程相结合,本文提出了一种新的粒子方法。数值结果表明,对于非均匀粒子分布的流体动力学,本文提出的方法具有可行性与良好的计算性能。

图:由MPS和本文提出的方法分别计算溃坝在t=0.6秒时流体的速度和压力分布情况:(a) MPS方法,(b) 本文提出的方法。
文四:

https://doi.org/10.1016/j.cma.2018.03.038
本文提出了一种近场动力学控制方程的弱形式,该形式允许直接施加非局部本质边界条件和自然边界条件。作者们还提出了一种变分的方法用以推导一点上场变量的一阶和二阶导数的近场动力学形式,这个点在其相互作用域上是非对称的。采用这种近场动力学的导数形式能将内力矢量和应力分量表达为非局部近场动力学形式且不需要任何校准过程。此外,它打消了人们对于靠近表面的材料点具有不完全作用区域的顾虑。因此,本文的解不受非局部边界力和表面效应的影响。本文所得方程的数值解可以采用非结构非均匀离散布点求解得到。作者们采用稳定双共轭梯度 (BiConjugate Gradient Stabilized, BICGSTAB)算法(一种求解稀疏非对称线性系统的迭代技术),实现了方程离散形式的隐式求解。显示分析是通过构造总体对角质量矩阵,并使用混合隐式/显式时间积分方案来实现。本文通过考虑平面应力条件下不同边界条件组合的弹性各向同性板,证明了该方法的正确性。
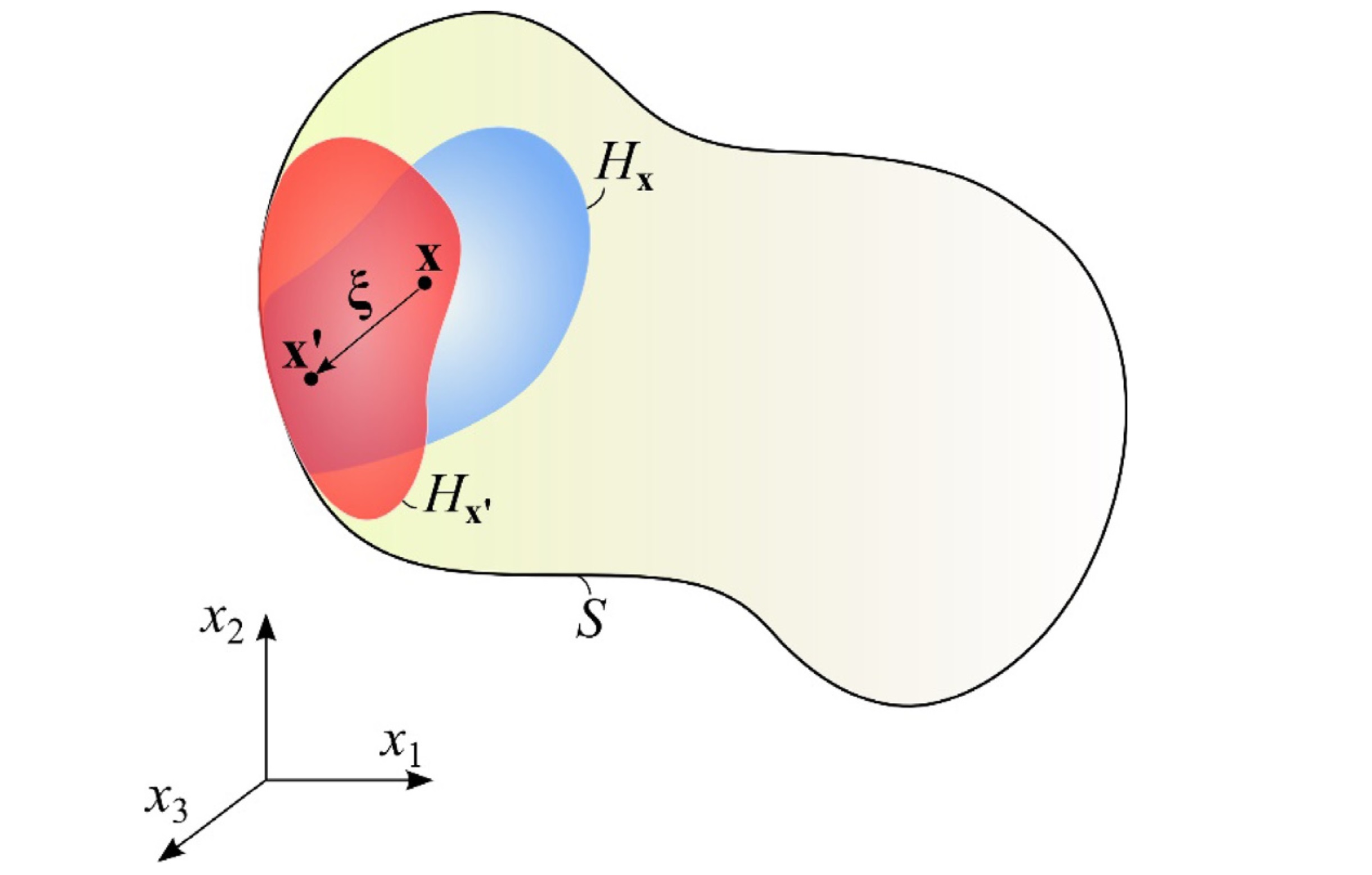
图:点x和x'在它们的任意形状相互作用域中的非对称位置。
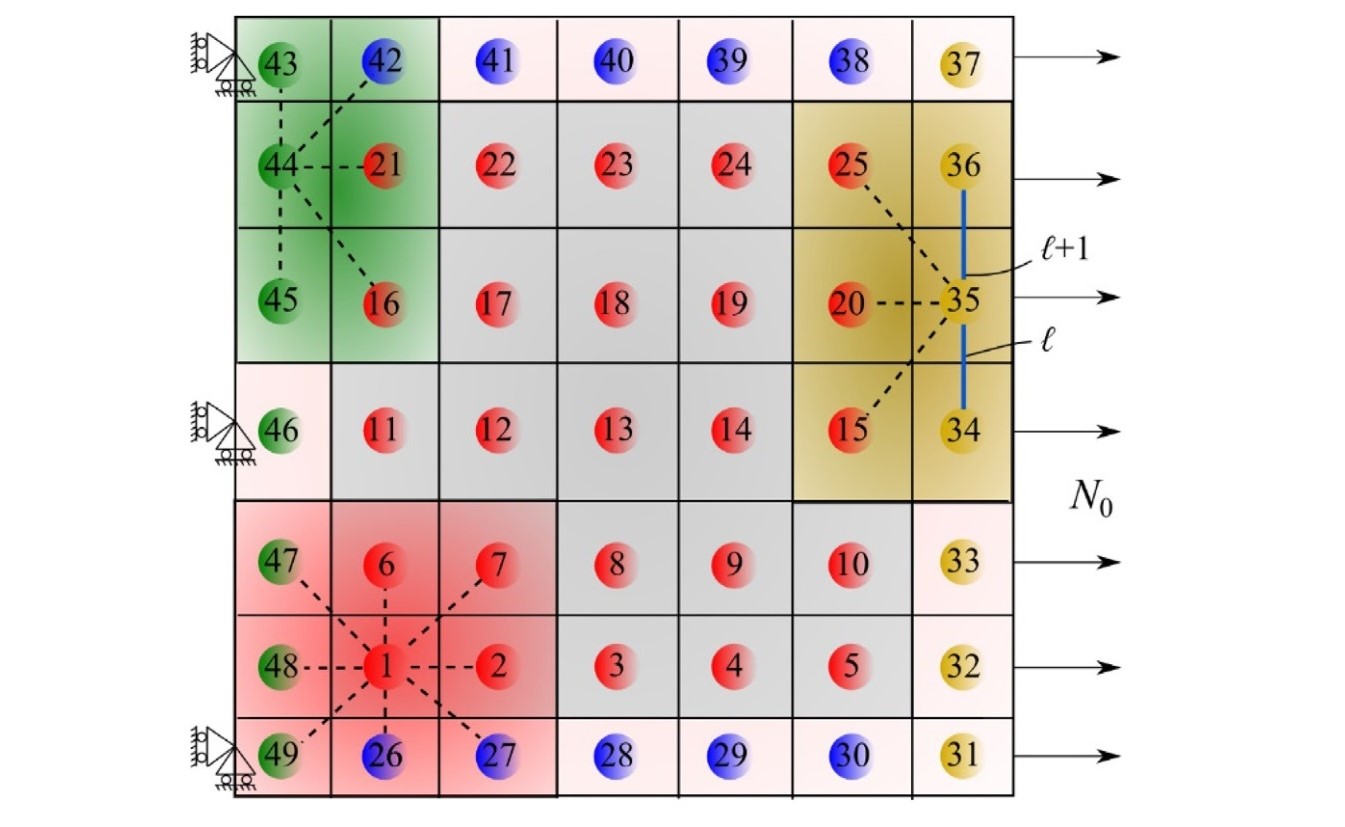
图:在施加面力和位移边界条件的情况下内部和边界点的耦合示意图。
文五:

https://doi.org/10.1016/j.engfracmech.2018.03.033
在有限元框架内,本文提出了一种的近场动力学单元用以分析变形和断裂。有限元节点之间的近场动力学相互作用通过桁架单元实现。应用这种单元可以对不规则形状的相互作用域和可变的近场作用邻域做非均匀离散。相互作用域的大小和形状决定了单元的连接性。这种连接性导致了一个稀疏的总体系统刚度矩阵。作者们采用稳定双共轭梯度 (BiConjugateGradient Stabilized, BICGSTAB)方法编写程序求解系统方程组。作者们通过构建一个总体集中质量矩阵和混合隐式/显式时间积分方案来实现显式分析。在裂纹萌生前,通过隐式求解器获得方程组的解,并在裂纹扩展过程中采用显式时间积分算法。当一个单元的最大主应力超过材料的单轴抗拉强度或(单元)可见性标准不满足时,材料会发生裂纹成核以及扩展的现象。通过考虑四种不同的几何构型(其中或包含或者不包含裂纹)以及不同的加载条件,作者们验证了本文所采用的桁架单元和失效准则的效果。在无裂纹扩展的情况下,作者们将近场动力学桁架单元的损伤预测结果与解析解和有限元的分析结果进行了对比。在有裂纹扩展的情况下,作者们将近场动力学损伤预测与现有的试验结果进行对比。
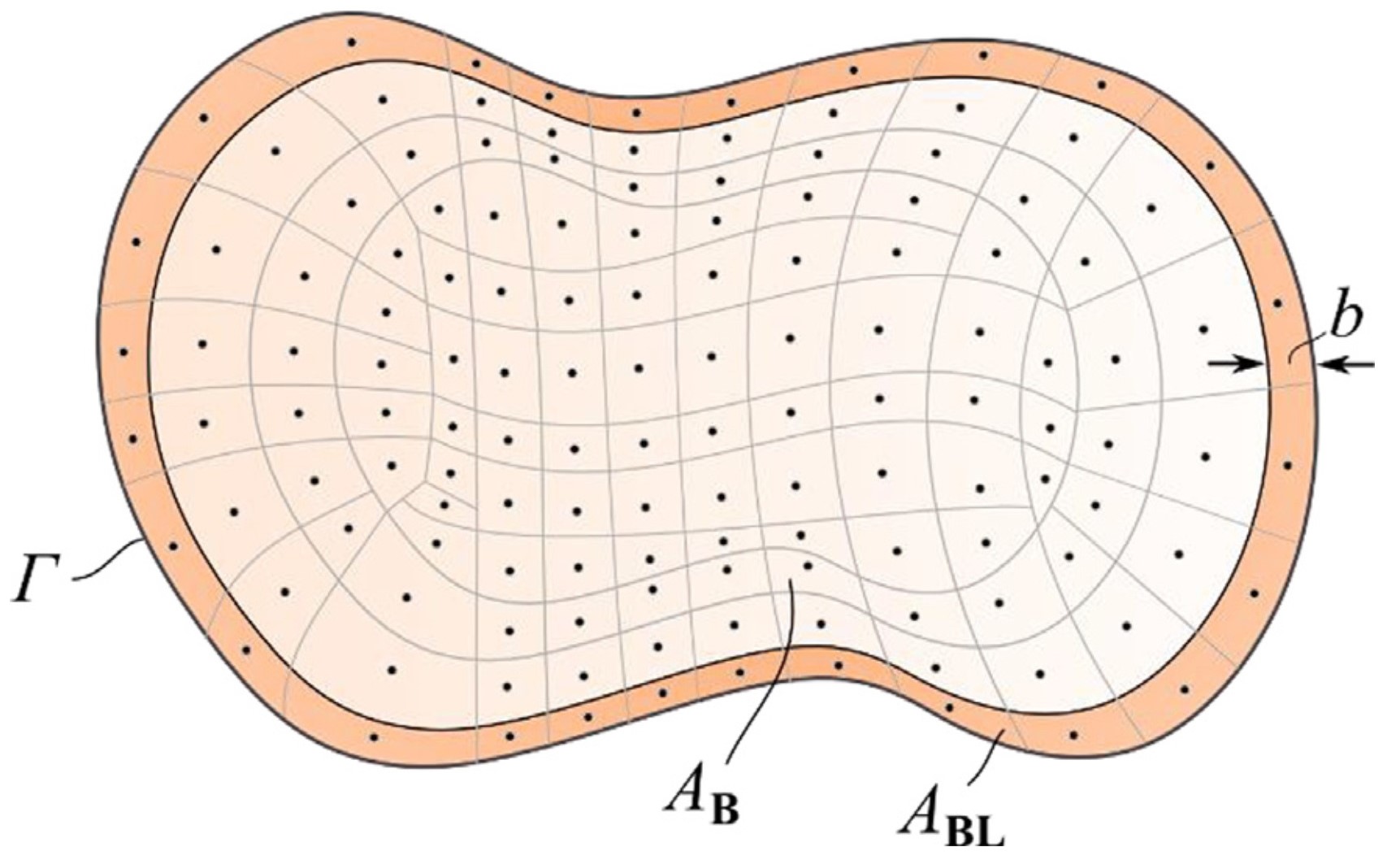
图:含内部AB和边界层ABL的近场动力学计算区域。
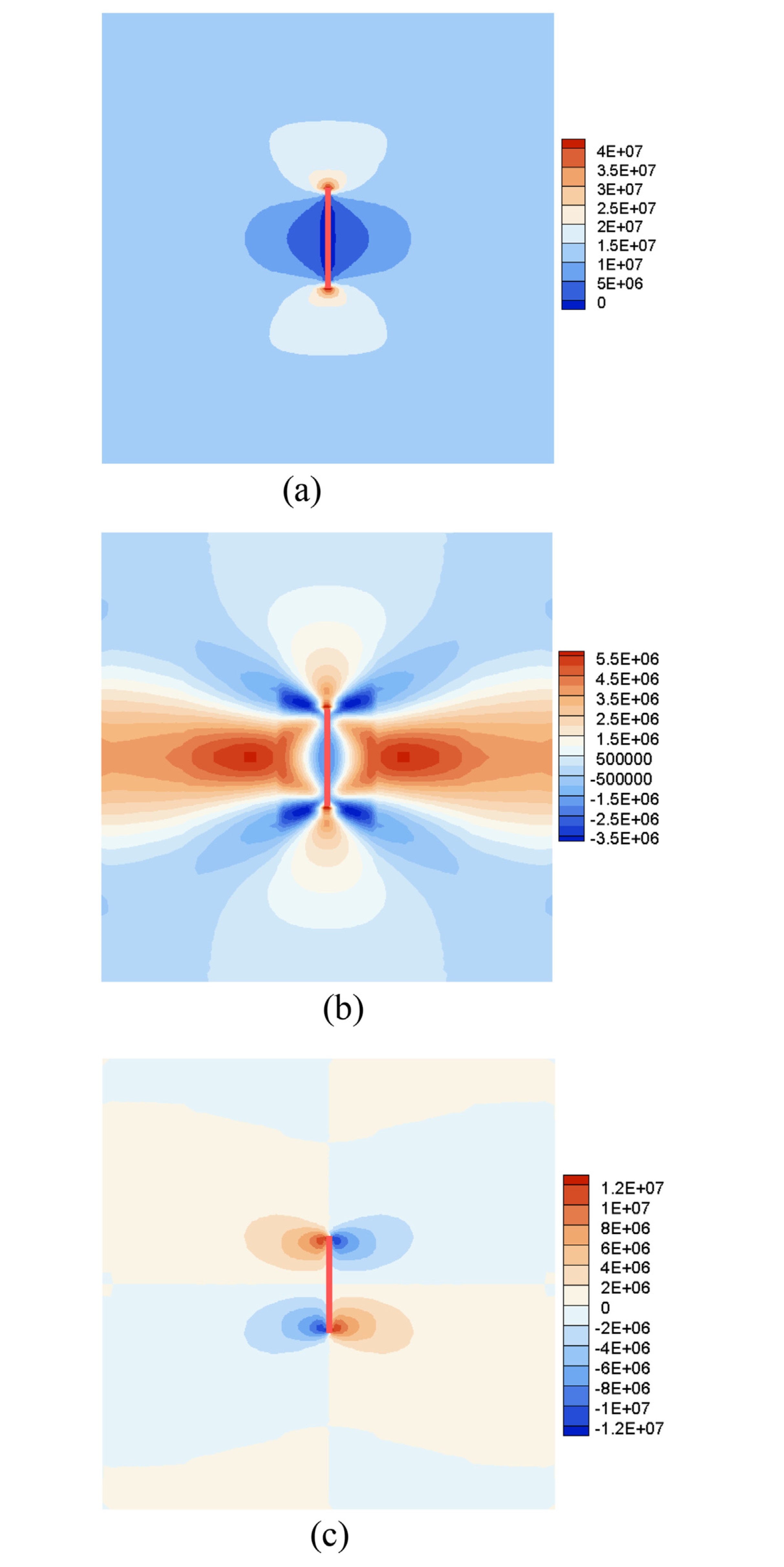
图:近场动力学计算的等效应力场云图 (a) x方向正应力,(b) y方向正应力,(c) 剪切应力。
————————————————————————————————————————————
近场动力学(PD)理论是国际上刚兴起的基于非局部作用思想建立的一整套力学理论体系,用空间积分方程代替偏微分方程用以描述物质的受力情况,从而避免了传统连续力学中的微分计算在遇到不连续问题时的奇异性,所以特别适用于模拟材料自发地断裂过程。然而,因为近场动力学的数学理论内容丰富且与传统理论差别较大,目前的相关文献又以英文表述为主,所以很多朋友在一开始学习时会遇到一些困难。因此,我于2016年9月建立了此微信公众号(近场动力学讨论班),希望通过自己的学习加上文献翻译和整理,降低新手学习近场动力学理论的入门门槛,分享国际上近场动力学的研究进展,从而聚集对近场动力学理论感兴趣的华人朋友,为推动近场动力学理论的发展做一点儿贡献!
https://blog.sciencenet.cn/blog-232936-1149157.html
上一篇:近场动力学最新上线的文章快报:2018年3月(下)
下一篇:近场动力学最新上线的文章快报:2018年4月(下)