每期文章评述的首发平台是微信公众号：近场动力学PD讨论班，也可以搜索微信号：peridynamics，或扫描文末的二维码加入。

2018年1月中期有五篇新文章上线（数据来源于谷歌学术，其中仅包括英文和中文的全文文献）。下面我按照上线的先后顺序依次简要介绍：

文一：

https://doi.org/10.1115/IMECE2017-71527
本文重新建立了基于不规则区域分解的经典键型近场动力学热力模型，并推导了相应的MOOSE-based隐式公式，其中MOOSE是Multiphysics Object-Oriented Simulation Environment。首先，作者们建立了基于不规则网格的近场动力学热力模型，并导出了模型参数。随后，对静态或拟静态问题的解给出了一个隐式公式，并针对MOOSE-based实现方面进行了阐述。然后，作者们通过热力问题的基准解进一步验证了公式。并采用不规则网格研究了高温时二维圆形和三维圆柱体核燃料中裂纹的开裂和传播。

图：使用不规则网格做二维模拟得到的最终裂纹分布

图：使用不规则网格做三维模拟得到的最终裂纹分布

文二：

https://doi.org/10.1016/j.crme.2017.12.014
本文研究了一个有限长度的非局部杆的静态和动态行为。文中考虑的非局部积分模型是应变型和相对位移型非局部模型，后者也可以看作是一个近场动力学模型。对于无限长介质，就充分光滑的位移场而言，通过假设一些内核对应规则，两种积分非局部模型可以是等价的。对于无限长介质（或者具有扩展反射规则的有限长介质），Eringen的微分模型可被重新推导成一个具有指数核的一致应变型积分非局部模型，或者是一个具有改进指数核的相对位移型积分非局部模型。作者们以承受均匀拉力的有限长杆作为静态情况下的一个范例。作者们应用文献中已有的不同核分析了在拉力作用下这个杆的应力型非局部行为。分析表明：为了保持与均匀应力状态相关的均匀应变场，这个核必须满足一些归一化和约束相容性条件。为了建立这样一个核，可以通过相容边界条件结合局部和非局部应变，或者在保留一些运动学相容性条件下扩展相应有限尺度外的区域。对非局部近场动力学杆得到了相同的结果，并且对在约束条件附近满足一致相容运动学边界条件的弹性杆，获得了一个解析的均匀应变场。最后，作者们把这些研究结果推广到两端固定有限长杆的振动，并且对应变型模型和近场动力学模型分别计算了固有频率。

文三：

http://kns.cnki.net/
近场动力学理论由于其可自然描述不连续及多尺度计算等优点，近年来在结构损伤模拟中得到了广泛的关注。复合材料在航空航天、船舶与汽车等国民重点领域中已得到普遍的应用，其各向异性材料特征及复杂的失效模式一度成为近场动力学理论研究的热门问题。通用复合材料模型的基本假设为：在单层板面内的键由纤维键和基体键共同构成，只有沿纤维方向的键定义为纤维键，其他方向都为基体键。通用模型假设尽管一定程度上在保证总体计算精度的情况下减小了计算消耗，然而推广至普遍情形时却无法完全反映复合材料的各向异性等特性，势必造成模拟不同角度纤维方向时具有较大的误差。本文针对通用模型的误差问题进行了细致的数值计算与分析，对比分析了三种修正方法，即：近场范围修正、近似取点修正以及球函数模型修正。修正结果对比显示，近场范围修正与近似取点修正方法都无法真正解决通用模型的误差问题，唯有新提出的球函数修正采用随角度连续变化的微模量函数有效减小了误差。

本文从能量等效角度出发，采用球函数表示的微模量计算得到近场动力学应变能密度，并与经典层合板应变能密度对比得到待定参数。编写相应的Fortran计算程序，采用经典 PMB材料模型并引入键最大“应变”失效准则。对各向同性材料板进行了弹性变形阶段的位移对比和收敛性分析及失效阶段的裂纹扩展模拟，与理论解或有限元结果进行了对比分析，说明了近场动力学方法模拟断裂问题的可行性与有效性。

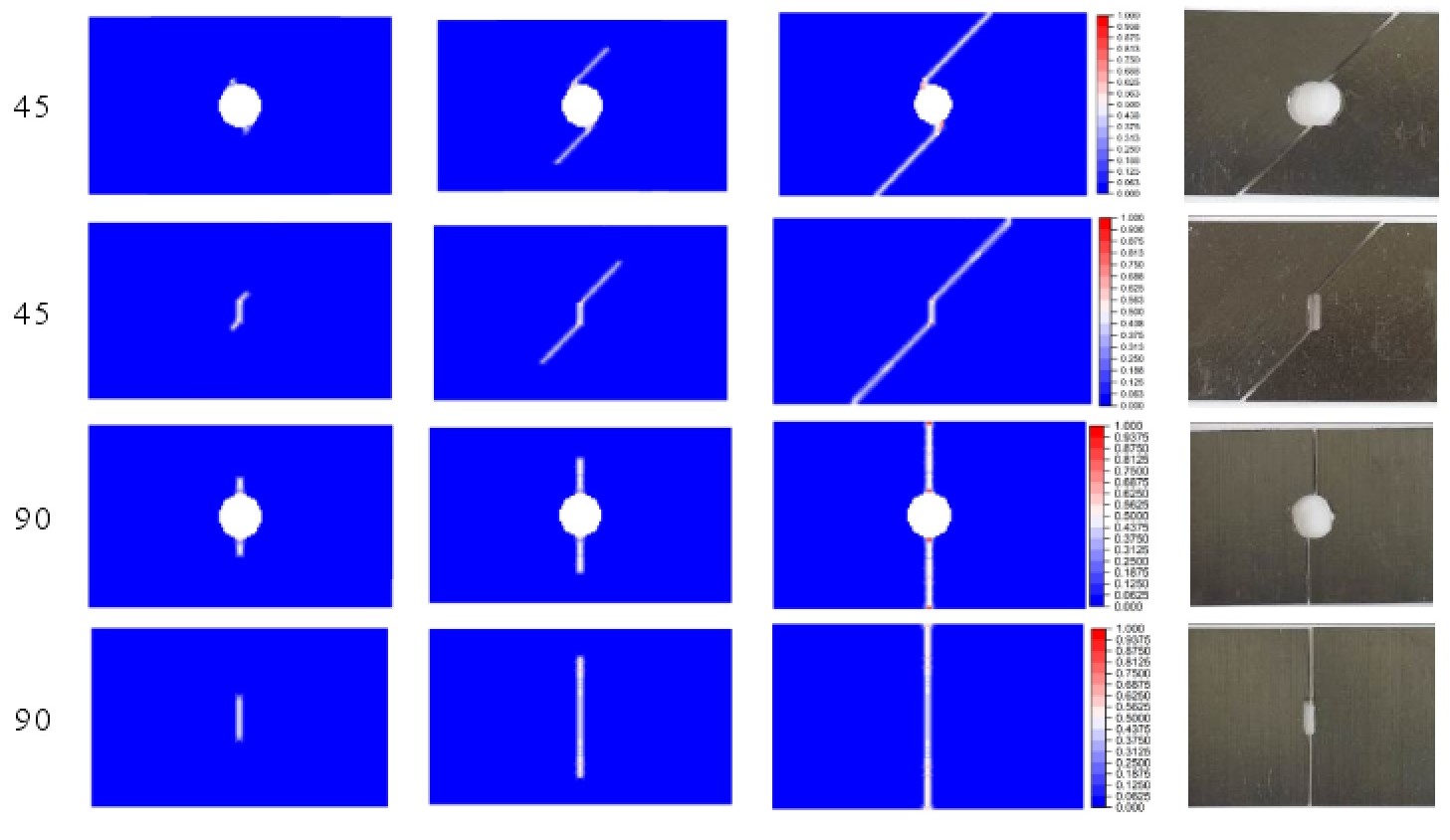
图：其他纤维向复合材料单向板渐进损伤过程

文四：

https://arxiv.org/abs/1801.04488
作者们针对具有径向核函数的紧支非局部微积分方程提出了一个无网格求积规则。作者们应用这个规则对一个要求无背景网格的近场动力学固体力学模型发展了一种强形式无网格离散方式。已有的近场动力学模型的离散方式对相应的线性弹性局部解一直存在渐近相容性缺失的问题。通过将求积规则设置为一个等效约束最小二乘问题，作者们通过重现性约束条件渐近地获得了一致收敛性。他们的方法对静态和动态问题自然地处理了无面力边界条件，表面效应和损伤建模。作者们通过比较人为解和已知解析解的具有裂纹奇点的情况证明了局部理论的高阶收敛性。最后，作者们通过重现从Kalthoff-Winkler实验获得的高速冲击结果证实了这个方法对实际问题的适用性。

图：Kalthoff-Winkler实验的几何和边界条件

图：1,100,200,300时间步后，Kalthoff-Winkler实验的裂纹演变过程，其中的云图是用lg||u||表示的位移场。

文五：

http://hdl.handle.net/10150/626361
地聚合物是一种新颖的胶结材料，它是一种潜在的能替代普通波特兰（硅酸盐）水泥的工程材料。然而，直到现在对于革新材料的研究还是只限于实验研究，而实验研究很难考虑到能对宏观性质起决定性作用的微细观结构和原子尺度上的机制。大多数针对地聚合物的实验研究主要考虑宏观性能且把地聚合物当作单项材料。然而，研究已经显示出地聚合物是一种包含地聚合物粘合剂（GB），未反应的源材料，源材料中的钙和水合硅酸钙（CSH）的复合材料。因此，本研究采用多尺度/多物理建模方法研究不同条件和不同尺度下的地聚合物结构和力学性能。作者首先使用分子动力学模拟决定地聚合物粘合剂、初级相和界面的力学性质。利用分子动力学模拟得到的性质，作者进一步使用近场动力学理论建立了地聚合物复合材料的细尺度模型，它能够考虑大颗粒的地聚合物粘合剂和分子动力学不易建模的纳米尺度初级相。作者将近场动力学模拟得到的结果直接与实验观测的力学性质进行比较。研究显示本文的模型可以直接用于构造更先进的地聚合物模型，并被用于设计超强地聚合物材料。

图：地聚合物粘合剂(GB)-水合硅酸钙(CSH)（钙/硅=1.45）复合材料失效界面(a)平行和(b)垂直于水合硅酸钙的二氧化硅层。

图：平均颗粒尺寸350纳米的地质聚合物的近场动力学模型：(a)未变形的初始模型，每一种颜色代表一个不同的颗粒项，每种颗粒项满足等概率和均匀分布；（b-d）子图是1%应变状态时，不同复合材料的损伤情况，其中蓝色代表未损伤，绿色代表损伤中间阶段，红色代表完全损伤。(b)地聚合物粘合剂(GB)-石英；(c)地聚合物粘合剂(GB)-水合硅酸钙(CSH)；(d)地聚合物粘合剂(GB)-水合硅酸钙(CSH)-石英复合材料。

———————————————————————————————————————————————

近场动力学(PD)理论是国际上刚兴起的基于非局部作用思想建立的一整套力学理论体系，用空间积分方程代替偏微分方程用以描述物质的受力情况，从而避免了传统连续力学中的微分计算在遇到不连续问题时的奇异性，所以特别适用于模拟材料自发地断裂过程。然而，因为近场动力学的数学理论内容丰富且与传统理论差别较大，目前的相关文献又以英文表述为主，所以很多朋友在一开始学习时会遇到一些困难。因此，我于2016年9月建立了此微信公众号（近场动力学讨论班），希望通过自己的学习加上文献翻译和整理，降低新手学习近场动力学理论的入门门槛，分享国际上近场动力学的研究进展，从而聚集对近场动力学理论感兴趣的华人朋友，为推动近场动力学理论的发展做一点儿贡献！

每期文章评述的首发平台是微信公众号：近场动力学PD讨论班
也可以搜索微信号：peridynamics

或扫如下二维码加入公众号：