博文
(力学领域研究热点)近场动力学漫谈(中):本构关系与运动方程
||
从上期的介绍中您已经明白了“键“和”态“的概念。键标定了两点之间的关联关系,具体讲是两点间的相对位置向量。态是向量的函数,定义了向量空间到张量集合的一个映射。态点积的定义是两个张量点积后的积分。
本期我们将会看到,基于键和态的概念,Silling博士等人在2007年的文章中(见如下文章标题),定义了两点之间的三种不同本构关系,即键基PD模型(Bond-based Peridynamic Model),常规态基PD模型(Odinaray State-based Peridynamic Model)和非常规态基PD模型(Nonordinary State-based Peridynamic Model)。

http://dx.doi.org/10.1007/s10659-007-9125-1
本构关系
在近场动力学理论中,本构关系主要是指力和键之间的关联关系,即力是键的函数。您可能会疑惑:为什么会有三种不同的本构关系呢?简单的讲,一根键在两个端点处各承受一个力,我们称之为力态。三种本构关系表现出不同的力态大小和方向。我们先从下图中直观地区分它们的不同之处(见图1):(1) 在键基(Bond based)PD模型中,两端点x 和 x' 上的力态是沿着两点之间的键 ξ,且大小相等、方向相反,即所谓的中心相互作用力。(2) 在常规态基(Ordinary state based)PD模型中,两个力态仍然是沿着端点 x 和 x' 之间的键 ξ 且方向相反,但是大小可以不相等。(3) 在非常规态基(Non-ordinary state based)的PD模型中,两个力态可以是任意方向且大小也不相等。
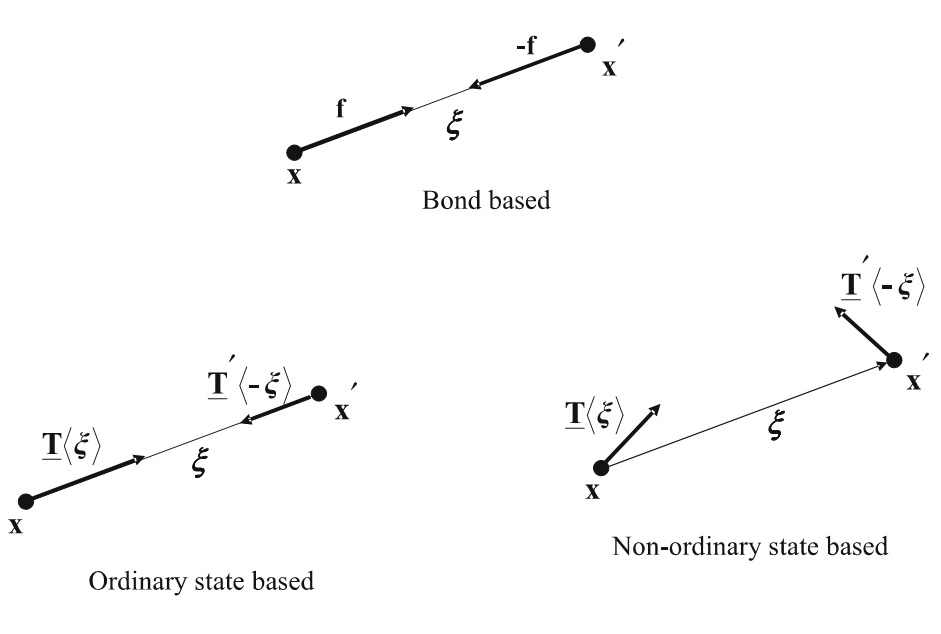
图1. 两点 x 和 x' 之间的三种基本的本构关系:键基(上)、常规态基(左下)和非常规态基(右下)模型。
我们再来对比三种本构关系的表达式(红框中的内容):

从上面三个红框中的力态表达式我们可以看到:键基PD模型的本构关系和常规态基PD模型的本构关系都是一个标量态乘以一个向量态。标量态表明力的大小,向量态表明力的方向。键基PD本构关系也可以等价地用张量和向量形式表示,即 f 的表达式。它仅与两端点的相对位置向量 ξ 和相对位移向量 η 有关,也因此两端点的力态大小相等且方向相反。相比较,常规态基PD本构中力的大小 t 由两项加和而成,第一项是点 x 周围的非局部作用邻域(近场作用范围 Hδ(x))的形变对力态的影响,第二项仅是键 ξ 的变形对该点力态的影响。两项的加和才是点 x 相关于键 ξ 的力态大小,而力态的方向与变形后的键方向一致,即键变形态 Y<ξ> 的方向。因为两端点的力态大小与各自周围的形变有关,但方向却都是由键的变形态决定,所以力态的大小不同,但方向沿同一直线且相反。从后面的证明中,我们还可以看到,键基PD本构其实是常规态基PD本构关系的特例(线性化表达)。非常规态基PD模型的本构关系是Piola应力张量(用变形前的参考构造表达的应力)和形状张量的乘积。ω 是在作用邻域内具有非零值的权函数。因为非常规PD本构的力态 T 由端点各自的Piola应力张量表达,所以两端点力态的大小和方向都可以不同。非常规态基PD本构关系建立起了键的力态与应力之间的关系,从而可以方便得计算裂尖处的应力。关于三种本构关系更详细的介绍请您阅读本期附录中的内容。
运动方程
下面我们来看近场动力学理论中的运动(平衡)方程:
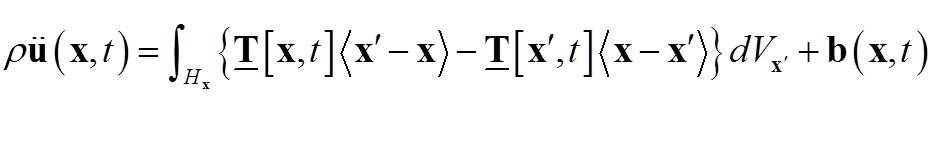
上面的公式中 ρ 是密度,u 是位移,b 是体力密度。力态 T 不仅是 ξ 的函数,即 T<ξ>。事实上,T 还是位置 x 和时间 t 的函数。因此,T 被记作 T[x,t]<x'-x>,其中x'-x=ξ 。在上面公式的积分号内,我们看到两个力态相减的形式。左手边的 T[x,t]<x'-x> 代表了在 x 点并由 x' 施加给 x 点的力,右手边的 T[x',t]<x-x'> 代表了在 x' 点并由 x 施加给 x'点的力 (也可以被记作T’<-ξ> 见上面图1)。两个力态相减代表了一种“相对”力的概念,也就是说,x 点承受由 x' 点施加给它的“绝对”力需要减去 x 点施加给 x'点的“绝对”力才是 x 点承受的由 x' 点而来的“净”力。然后再在点周围的邻域内进行积分,才得到该点所受的合力。打个比方:某厂家一年从市场上销售A类商品获得的收入,还需要减去从市场上购买制造A商品的原材料所花费的成本,才是该厂家一年在A商品上所得“净”利润(不考虑其他成本)。如果再对该厂家本年生产和销售的所有产品的“净”利润进行统计(在这里是作用邻域内积分),就得到了该厂家一年所得的全部收益,这个收益才是驱动该厂家进一步发展的“合力”。
我们进一步用下图来解释一点 x 与其周围作用邻域内点 x'的相互作用力(图3 左图)和该点在区域 Ω 内的作用邻域 Hδ(x)(图3 右图),该区域承受体力 b。
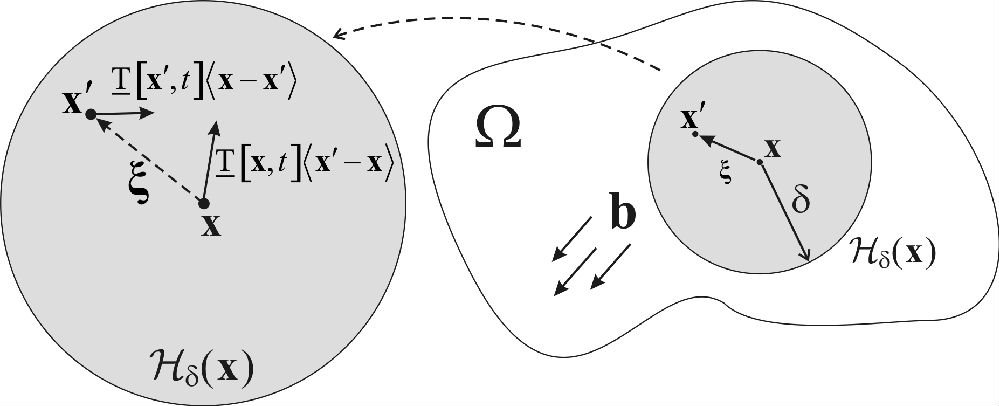
图3. (左)点 x 与 x' 的相互作用力态,(右)点 x 在区域Ω 中的作用邻域
从上面的运动方程中我们还可以推测出力态的量刚:在三维情况下,两力态的差在球形作用邻域上积分后的单位与体力密度的单位一致,即牛顿/米的3次方。因此,我们就知道力态的单位应该是牛顿/米的6次方。这是和传统的力密度不同的地方。在附录中,从力态的具体表达式您也可以直接推出这个结论。
键的断裂准则和等效断裂功
目前,最常见的一种键的断裂准则,是由Silling博士等人于2005年在下面这篇文章中提出的PMB材料(Prototype Microelastic Brittle material)模型。

http://dx.doi.org/10.1016/j.compstruc.2004.11.026
为了上下文符号统一,我把文章中的公式用态的形式进行了重新书写,表达如下:

其中 M(Y)<ξ> 是键的方向态,Y<ξ> 是键的变形态,X<ξ>=ξ 是单位向量态,也就键本身。t 由三项的乘积组成:c 是系数,s 是键的伸长率,μ 用来控制键是否断裂。当键的伸长率小于某个阀值 s0 时,μ=1 表明键完好无损,否则 μ=0 键完全断裂,且不可恢复。这里 t 和 t' 是计算时间。我们还可以用下图(图4)来展示 t和 s 的取值关系,以说明键的断裂过程:
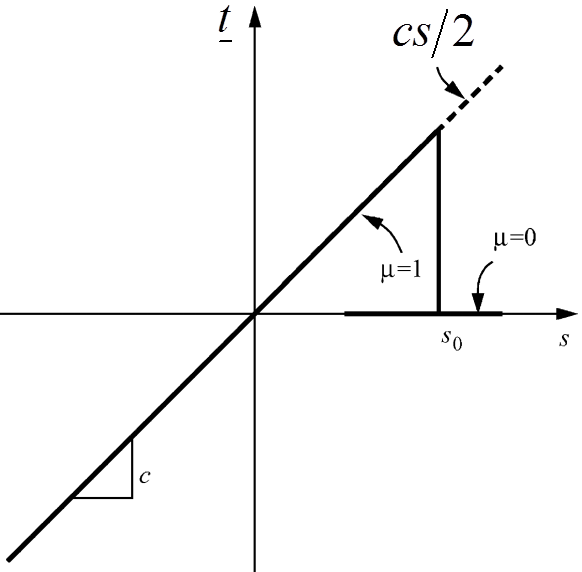
图4. 在PMB材料中力作为键的伸长率的函数
有了上面的断裂准则,我们还可以计算三维体裂纹面上单位面积的等效断裂功:

我们可以借助下图5来说明等效断裂功的计算方法:δ 是一点 x 的周围邻域的作用半径。我们定义所有穿越断裂面的键都要断开。那么,长度为 δ 的红线上的所有点,他们穿越断裂面(上面半圆形的底边)的键断开时所拥有的键断裂功的总和即为断裂面上绿色点处的等效断裂功。对于红线上的任意一点 A,它的任意一根键的断裂功等于该键的伸长率达到 s0 时所包含的能量(不同的键长有不同的能量,即使伸长率相同)。更为详细的内容请您查阅原文。
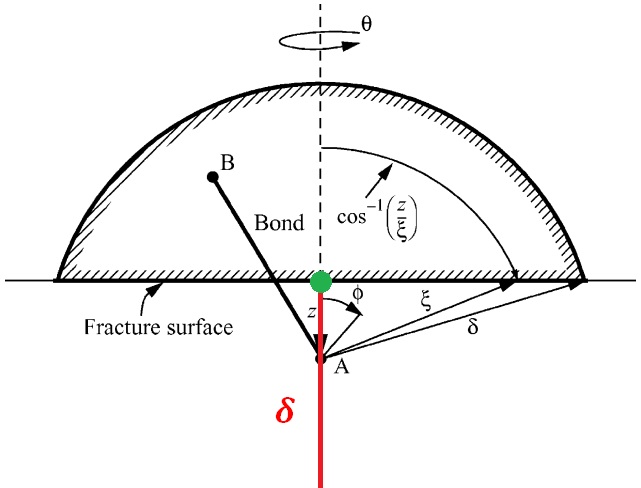
图5. 计算三维体裂纹面上单位面积的等效断裂功
上面所介绍的根据键的伸长率来判定断裂的准则,仅仅是目前已经提出的若干种键断裂准则中的一种较为常用的准则。除此之外,其它的键断裂准则,如:(1) 随着键的伸长力逐渐衰减的软化准则 [3];(2) 根据键的变形能判定键断裂的准则 [4] 等。由于篇幅有限,我们不再详述。
动量和能量守恒
除上面所讲的本构关系、运动方程和键断裂准则以外,还有一部分关于动量和能量守恒律的内容需要在此提及,但是由于篇幅有限,本文不展开讨论。2010年,Silling博士及其合作者写了一篇关于近场动力学的总结性文章《Peridynamic Theory of Solid Mechanics》[5],其中的第2章讨论了与近场动力学模型相关的线动量守恒律,角动量守恒律,虚功原理以及能量守恒(热力学第一定律),在文章的第4章第5节还讨论了热力学第二定律对于建立本构关系的限制。这些内容从全局的动量和能量守恒的维度来认识近场动力学模型。在这个维度上,近场动力学模型和传统的力学模型有很多相通的地方,也因此是一个好的视角从与传统模型的比较中认识近场动力学模型。
您或许能从如下近场动力学模型和经典理论模型的对照表里获得更多、更深刻的理解。

附录:三种本构关系详述
您将依次看到三种本构关系的详细解释,其中在常规态基PD本构关系(第2种本构关系)中,我还简要介绍了如何由能量密度表达式推出本构关系表达式,以及如何通过线性化过程从常规态基PD本构关系中推出键基PD本构关系。

键基PD模型是一种形式相对简单的PD模型,我们可以仅用张量和向量的形式来表示。而且力 f 是相对位移向量 η 的线性函数(在上文第3部分关于键的断裂准则一节中,我们还看到了一种非线性的键基PD模型,即PMB材料的本构)。从后面常规态基PD本构关系的论述中我们还可以看到:键基PD本构关系实际上是常规态基PD本构关系的特例并线性化形式,其中指出力态 T = f,并且力的方向与键 ξ 的方向始终一致,上面我们也论述了两端点上的力大小相等、方向相反。这种键基PD本构关系是目前文献中使用较多的一种,然而值得注意的是这种模型的等效泊松比只能是固定值,如三维情况下只能是1/4。关于键基PD模型的更多内容讨论,请参考Silling博士发表于2000年的首篇近场动力学文章。目前在公众号“近场动力学PD讨论班”(扫描文末的二维码)中也已经刊出了该文章的系列评述。
下面我们来看常规态基PD模型(Ordinary State-based Peridynamic Model):

在上面的公式中,我们先给出基本态变量的定义,关于态变量的详细说明请参考上期《近场动力学漫谈(上):键与态》。Y<ξ> 是键的变形态表达了变形后键的两个端点 x 和 x' 之间的相对位置,其中 x'=x+ξ,u 表示位移。X<ξ> 是单位向量态,是 ξ 本身。x 是键的长度,e 是变形后键的长度减去变形前键的长度,表示键的伸长量。ω<ξ> 是在非局部作用邻域(近场作用范围 Hδ(x))内部具有非零值的权函数,通常情况下,我们会应用 ω<ξ> = ω<|ξ|>,此时 ω 被称为是球形权函数 [1]。那么,在常规态基PD模型中,本构关系如下式所示:

在上面的本构关系中,T 是一点上所承受的力态,力态也是一个向量态。t 是一个标量态,它表示了力的大小,M 是一个向量态,它是变形态 Y<ξ> 的函数,被详细的记作 M(Y)<ξ>, 它表明了变形态 Y<ξ> 的方向。因此,我们可以简单得理解作:在常规态基PD模型中,一点上所受的力(态 T)等于力的大小(t)乘以力的方向(M)。而且,这个力态的方向一直是和变形后键的方向一致。
我们先来解释 t 的表达式中的两个变量 m 和 θ。 m 和 θ 都是实数,在这里我们不讨论权函数 ω 的影响。那么,m是键长求平方后在一点的作用邻域上的积分。如果长度是以米为单位,那么在三维情况下,m 的单位是什么? 从上面态点积所代表的积分式我们可以看出, m 是键长的平方再在球形邻域上积分,我把这个积分值看做是变形前的标准体积。实际上,在三维情况下 m 的单位应该是米的5次方。我们再来看变量 θ, θ 是键的伸长量 e 的函数,从 θ的表达式我们可以简单的理解为:键的伸长量与键长的乘积后再在一点的邻域内积分,我把这个积分值看作是体积的膨胀量。它再除以 m 即得θ,所以θ可以被简单得理解为一点周围体积的膨胀率。 除此之外,在t的表达式中还有两个材料参数 λ 和 τ,它们相当于键的弹性模量,与经典弹性力学的杨氏模量和泊松比具有关联关系,具体的转换公式参见 [2]中附录,也就是说它们的单位是牛顿/平方米。那么,请您思考力态 T 的单位。在三维情况下,一个力态 T 的单位是牛顿/米的6次方(传统的体力密度是牛顿/米的3次方)。
让我们再来看t 的表达式,t由两项组成,前一项中含有体积膨胀率θ 代表了一点周围体积的变形对该点的键 ξ 上的力态的影响,它包含了一点周围所有的键的变形对该点的作用(如上面公式中的蓝色虚线箭头所指的示意图显示:圆形区域内的所有蓝色点对中心点受力的贡献),后一项中含有键 ξ的伸长量 e,代表单键 ξ 的变形对该力态的影响。
本构关系的推导过程:
那么,这个本构关系是如何得到的呢?我们知道在经典力学中应力是弹性能对应变的广义变分。相似地,在近场动力学里,一点 x 相关于键 ξ 的力态是变形能对键的变形量的广义变分,只是这里的变分需要用到我们上期提到的广义弗雷歇导数。具体内容请参考2007年的文章 [1]。我们用下面的公式简单推导:在这里我们先直接给出一点的能量密度泛函(详细表达式请参见上期《近场动力学漫谈(上):键与态》中的内容)。类似于经典弹性力学,这个能量密度表达式在Silling博士2007年发表的文章中被写成了体积膨胀项(dilatation)和偏应变项(deviatoric)的和(参见Silling2007年的文章 [1]),我在此基础上将其写成如下的这个等价表达式(具体推导过程参见我的文章 [2])。在Silling博士2007年的文章中已经详细证明了标量态t可以表达为能量密度泛函对变量 e 的广义变分。再根据能量密度泛函的具体表达式,我们就可以得到t的详细公式。

从常规态基PD本构关系中推导出键基PD本构关系:
至此,我们已经了解了键基PD本构关系式和常规态基PD本构关系式。实际上,键基PD本构可以被看做是态基PD本构的一个特例(不考虑体积膨胀对于力态的影响,仅考虑单键的变形对力态的影响)。现在简单推导如下,具体过程请见参考文献 [2]。

从上面的公式,我们可以看到,若不考虑一点周围的体积膨胀对该点力态的影响,而仅剩下单键上的伸长量对力态的影响。即,在t 的表达式中除去第一项,保留第二项。再对 e 和 M(Y)<ξ> 分别进行线性化处理(参见下图2),e 的大小仅与键 ξ 两端点的位移差 U 相关(这里 U 和 η 相同,它们分别是相对位移的向量态表达和向量表达),M 表示键 ξ 变形后的方向近似等于键 ξ 本身的方向,代入力态 T 的表达式,经过代换后我们发现 T = f,从而推出键基PD的本构关系。从下面这个几何图示中我们可以了解到更多关于e 线性化的近似过程。当夹角 Φ 趋近于 0 的时候(即小变形假设成立),这时ξ 与 Y<ξ> 几乎重合,则e 满足如下关于两端点位移差的近似线性关系:
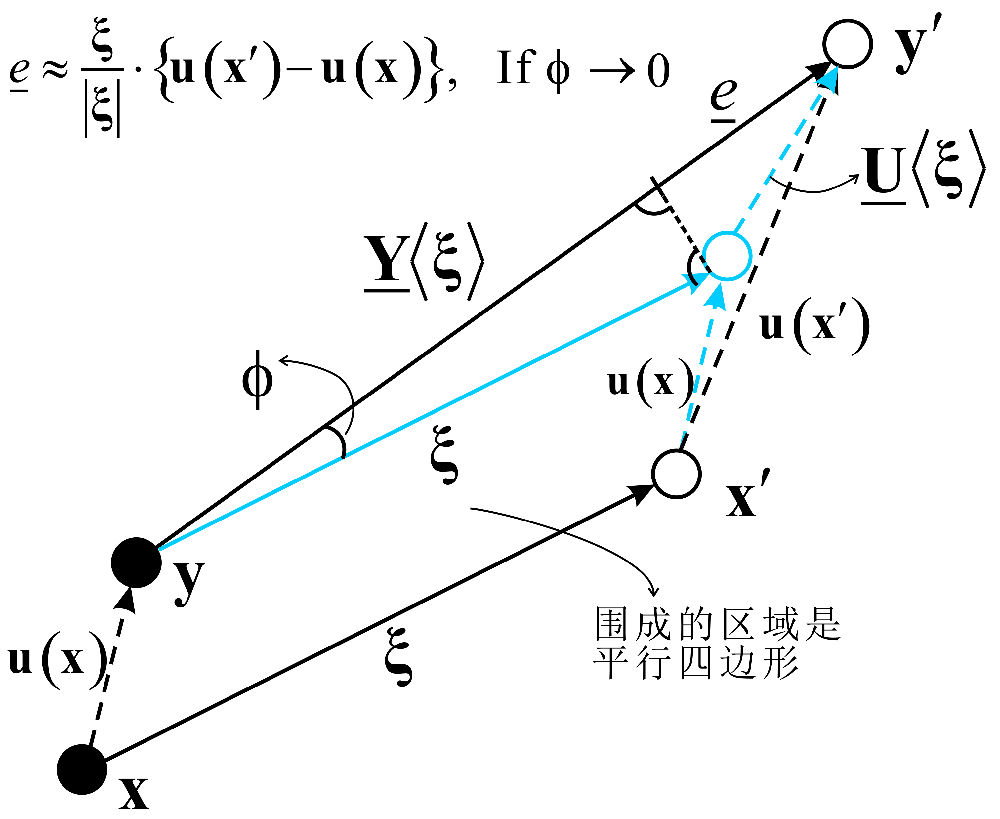
图2. 键 ξ的伸长量e 与近似表示的几何示意图
做上面这个简化推导的目的是为了将键基PD本构和态基PD本构统一起来。
最后介绍非常规态基PD模型的本构关系。

上面给出了非常规态基PD模型的本构关系的基本公式。所谓非常规的意思,我个人的理解是在键的力态中引入了Piola应力张量和形状张量,而且确确实实是张量而不是态,这和之前讨论的常规态基PD模型不同。那么,我们先来看下面的几个变量:X是单位向量态 X<ξ> = ξ,K 是周围邻域内的所有 ξ自身做张量积后再积分,称之为形状张量。F 是PD中的变形梯度张量。我们知道 Y 是键的变形向量态,即变形后两端点的相对位置向量。从 F 的公式我们就可以直观的理解为变形后的形状张量比上变形前的形状张量(相当于单位张量再加上应变张量),这与传统连续介质力学中的变形梯度张量的表达类似。最后我们可以看到,这里的Piola应力张量有类似于传统连续介质力学的表达式,其中 τ (希腊字母Tau) 是柯西应力张量,det F 是行列式的值,上标 “-T” 代表了张量的逆的转置。通过这些运算公式,我们就可以计算出每个键上的力态,而且非常规PD模型建立起了键上的力态与端点上的柯西应力张量τ之间的关系,使得近场动力学和传统的连续介质力学模型联系起来,以便计算裂纹尖端处的应力。也正是因为力态 T 是应力的函数,因此T 的方向才可能是任意的。
参考文献:
[1] Silling,S.A., et al., Peridynamic states andconstitutive modeling. Journal of Elasticity, 2007. 88(2): 151-184.
[2] Han,F., et al., A morphing approach to couplestate-based peridynamics with classical continuum mechanics. ComputerMethods in Applied Mechanics and Engineering, 2016. 301: 336-358.
[3] Silling,S., et al., Crack nucleation in aperidynamic solid. International Journal of Fracture, 2010. 162(1-2): p. 219-227.
[4] Foster,J.T., S.A. Silling, and W. Chen, An energy based failure criterion for use with peridynamic states. International Journal for Multiscale Computational Engineering, 2011. 9(6): p. 675-687.
[5] Silling,S.A. and R.B. Lehoucq, Peridynamic Theory of Solid Mechanics, in Advances in Applied Mechanics, Vol 44. 2010, Elsevier Academic Press Inc: San Diego. p.73-168.
——————————————————————————————————————————————————
近场动力学(简称PD)理论是国际上刚兴起的基于非局部作用思想建立的一整套力学理论体系,该理论通过求解空间积分方程描述物质力学行为,避免了基于连续性假设建模和求解空间微分方程的传统宏观方法在面临不连续问题时的奇异性[1],所以特别适用于模拟材料的损伤和断裂过程。然而,因为PD模型的数学理论较深,且新概念多用英文表述,所以很多朋友在学习时会遇到一些困难。在朋友的启发下,我想到在微信上建立此公众号,希望将研究PD理论的朋友们聚集起来,分享PD研习路上的点点滴滴,一起解决各自的难题,共同推动PD理论的发展!
[1] 黄 丹, 章 青, 乔丕忠, 沈 峰, 近场动力学方法及其应用. 力学进展, 2010. 40(4): p. 448-459.
每期文章评述的首发平台是微信公众号:近场动力学PD讨论班
也可以搜索微信号:peridynamics
或扫如下二维码加入公众号:

https://blog.sciencenet.cn/blog-232936-1039884.html
上一篇:近场动力学漫谈(上):键与态
下一篇:近场动力学漫谈(下):数值方法与应用软件