博文
近场动力学漫谈(上):键与态
||
近场动力学(Peidynamics, PD)理论是基于非局部作用思想建立的一整套力学理论体系,该理论通过求解空间积分方程描述物质力学行为,避免了基于连续性假设的传统模型在面临不连续问题时的奇异性和复杂性,成功应用于不同尺度各种不连续问题的模拟中,已成为当前国际计算力学及相关领域的研究热点。
我将用三期的内容对近场动力学理论中的一些概念和方程做一个简要的介绍:(上)键与态,(中)本构关系与运动方程, (下)数值方法与应用软件。
近场动力学是由美国Sandia国家实验室的杰出研究员Stewart Silling博士于2000年提出的。从提出到现在的17年间,近场动力学经历了一个逐渐加速的发展过程。我选取了几篇个人认为在近场动力学的发展过程中有里程碑意义的文章,并从中挑选出重要的概念和方程加以介绍。通过这几期的学习,我们可以了解到近场动力学的一些基本知识。
键的概念
Silling博士于2000年发表了他的首篇近场动力学领域的开创性文章:

http://dx.doi.org/10.1016/S0022-5096(99)00029-0
在这篇文章中,Silling博士首次命名了这个理论,称为“Peridynamic”。这个词取自希腊文的两个词:“Peri”和“Dynamic”。"Peri"是附近,周围的意思,“Dynamic”原意是指力。据我所知,河海大学的章青教授于2010年在《力学进展》杂志上发表文章《近场动力学方法及其应用》应该算是首次在中文学术刊物上将“Peridynamics”译做“近场动力学”。关于“近场动力学”这个名字更为详细的介绍,请您查看《体会近场动力学之“动”》。
在Silling博士开创性文章的引言中,他论述了为什么要做近场动力学模型的原因:传统的连续介质力学在遇到位移场不连续的情况时(如含裂纹的材料)和遇到应变场不连续的情况时(如复合材料中的界面),在不连续处存在导数没有定义的情况,因此产生求解的困难。近场动力学通过建立积分方程,避免了这种奇异性,把连续和不连续的描述统一起来,并且带来了一个好处是可以模拟裂纹自发得萌生和扩展的过程。这里强调“自发(spontaneously)”是为了区别于以往的计算模型的情况。在以往模型的计算中,每一个计算步都需要判定裂纹继续扩展的条件并更新裂尖的扩展方向,随着裂纹的扩展还需要重新划分网格,或者在计算前需要选用特殊单元限定裂纹将要出现的位置(如cohesive单元)等,至于多裂纹扩展,裂纹分叉或合并等情况在以往数值模型的模拟过程中就更为复杂。而正如下面刚性球撞击脆性板的模拟动画的截图所示,在近场动力学模型的模拟过程中,裂纹的萌生、扩展、分叉等现象都是随着模拟过程自然而然产生的,除加入单一的键断裂条件,不需要过多的判定条件或特殊单元。
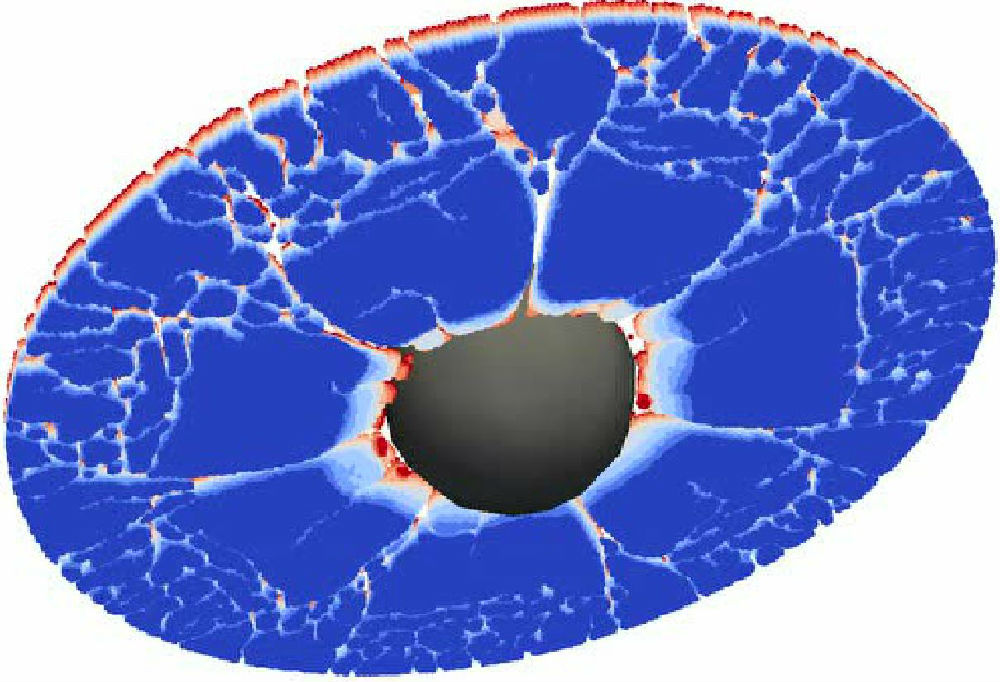
近场动力学模型模拟的刚性球撞击脆性板的过程
以上这个模拟过程是如何做到的呢?实际上,在近场动力学理论中,Silling博士首先建立了“键(bond)”的概念,键表达了一定范围(horizon δ)内两个点之间的关联性,具体是指两个点在几何上的相对位置向量(如下图1中 ξ 所示)。当变形发生以后,这两点之间的相对位置向量记作 Y<ξ>(字母下加下划线表示态的概念,我们下面会讲到),Y 是 ξ 的函数,表明键 ξ 的变形情况 (见图1中右图)。
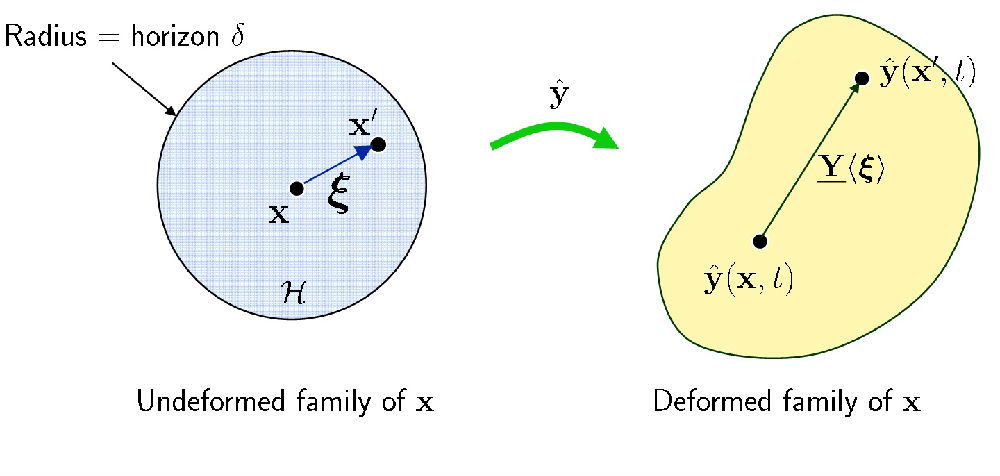
图1. 点 x 与 x' 之间的键 ξ,以及键 ξ 的变形 Y<ξ>,Y表示变形后两点的相对位置。
每个点 x 都和它周围的 δ 半径范围内的所有点具有键关联上的相互关系。当变形发生时,有些键的变形大,有些键的变形小。如下图2所示:
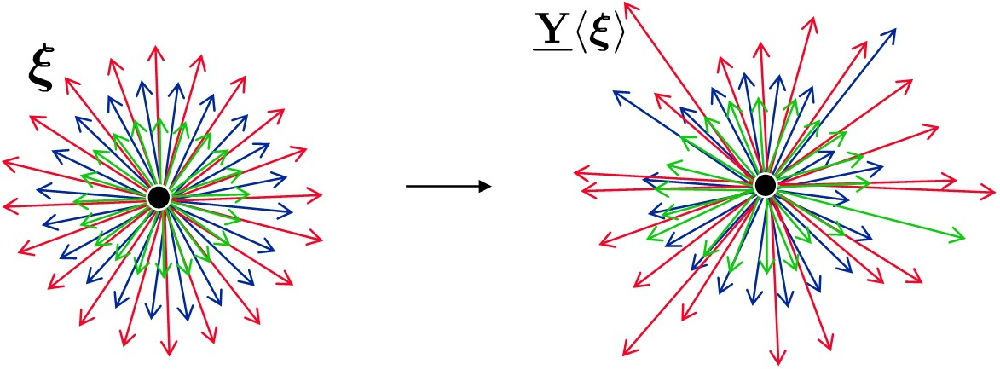
图2 一点周围的键及其键的变形
对于所有的键,人们事先只需要定义统一的键断裂准则(与 Y 的变形相关)。一种简单的键断裂准则为:当键的伸长率大于某个临界值时,键即刻断裂且不能再恢复。当键断裂后,表明键的两个端点不再具有相互作用。至于在模拟过程中,哪根键先断哪根后断,完全由几何结构、加载条件和加载历史决定。当有键开始断裂时,微裂纹就开始了萌生,当有一系列的键断裂后,由这些断裂键所形成的不连续空间就是宏观裂纹了。如下图3所示:
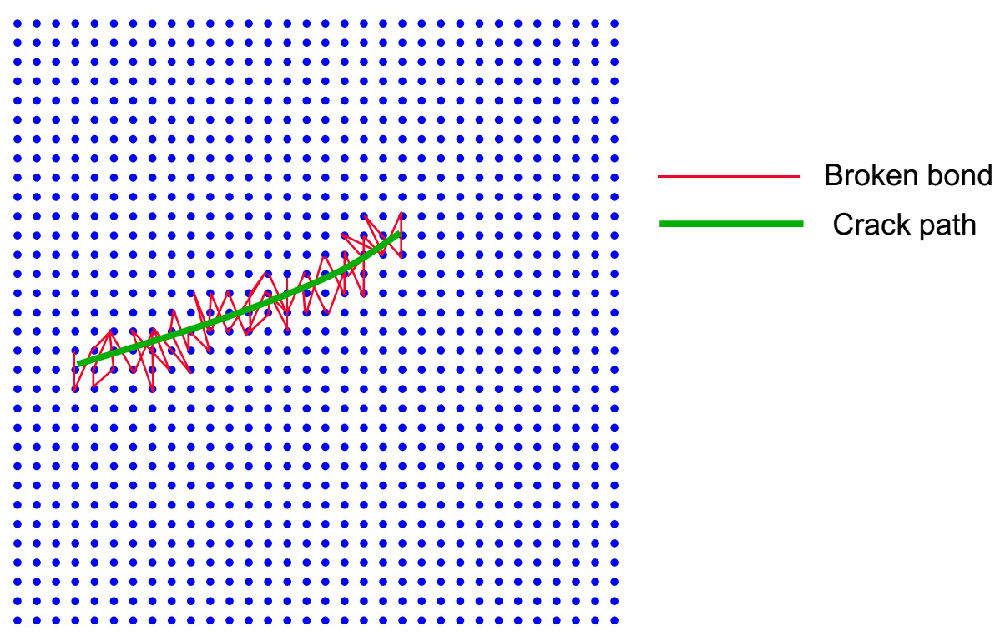
图3 断裂后的键形成了裂纹区
这篇开创性的文章提出了目前我们所谓的键基PD模型(Bond-based Peridynamic Model),我们在下一期中会详细介绍。文章从各向同性、弹性、本构模型的线性化、材料的稳定性分析、波的传播分析、加载条件等诸多方面对该模型的特性进行了论述。目前,我们针对这篇文章在微信公众号(参见文末的二维码)中推出了系列的评述文章《重构弹性理论的公式》,详细解读了文章的内容并细致推导了文章中的公式。对该文章感兴趣的朋友,敬请查阅相关内容。
然而,键基PD模型假设两点间的力是一种中心相互作用,即两点间的作用力沿着两点的连线,大小相等、方向相反(具体请参阅我们下期的内容)。这种中心力本构模型产生的一个限制性的后果就是材料的等效泊松比只能是定值,比如,键基PD模型等效的三维各向同性均匀弹性体的泊松比只能是1/4。
态的概念
为了解除固定泊松比的限制,Silling博士及其合作者发表于2007年的文章中发展出了新的本构模型:态基PD模型(State-based Peridynamic models)。(感兴趣的朋友可以参考下面这篇2007年发表的文章)

http://dx.doi.org/10.1007/s10659-007-9125-1
要讲态基PD模型,我们就不得不先解释什么是“态(state)”。态是Silling博士及其合作者们提出的一个数学概念,更具体得讲是一个向量空间到张量集合的映射。这样讲可能您就越发得不容易理解。那么我们换一种回答方式,看看是否能更容易理解:
问:为什么要建立态的概念?答:因为在近场动力学理论中需要用“态”替换掉经典弹性理论中的“张量”。
再问:为什么要在近场动力学中替换掉“张量”?再答:因为张量只能提供一种连续(光滑)的空间映射。比如变形梯度张量。而近场动力学理论需要一种连续(光滑)和不连续(不光滑)同时兼顾的空间映射。比如近场动力学里的向量态(我们下面会讲到)。
这里先给出态的基本数学定义及举例。

举例说明(理论上讲,态的数学定义可以到任意阶张量,但是近场动力学理论里用得最多的就是标量态和向量态):

上面最后一个公式是关于键的变形态的表达式,其中u是位移,x' 和 x 是键 ξ 的两个端点。我们可以用下图(图4)来进一步说明键的变形态(向量态):

图4. 键未变形时的向量态 X<ξ> 和键变形后的变形态(向量态)Y<ξ>,其中x' 和 x 是键 ξ 的变形前两端点的位置,y' 和 y 是键 ξ 的变形后两端点的位置
到此,您可能已经对键的变形态有所了解,其实说白了,就是变形后两点的相对位置向量。但是,您或许还一直对我之前的回答存疑:为什么说张量只能提供一种连续的空间映射,而态可以提供一种连续和不连续同时兼顾的空间映射呢?下面我们接着用图示的方式来对比二阶对称张量和向量态对向量空间的变换:
先以变形梯度张量为例,它的定义如下:

从下面示意图(图5)中我们可以看到一个变形梯度张量通过点积的方式将一簇向量连续映射到另一簇向量。
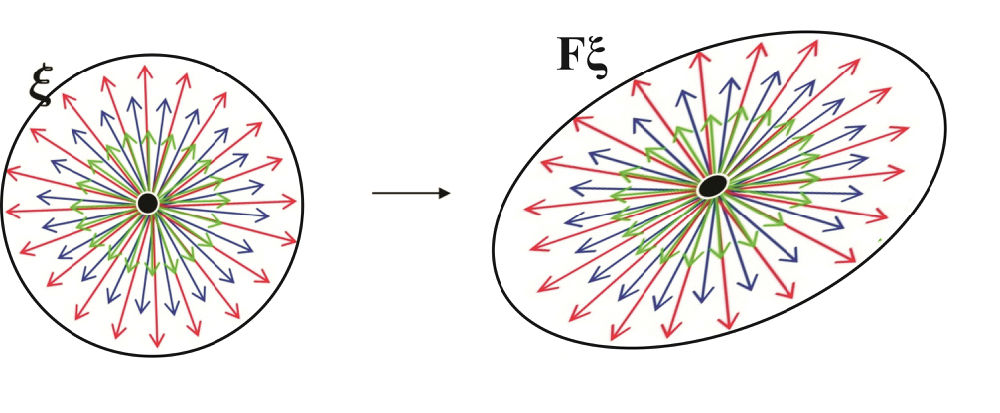
图5. 变形梯度张量F将一簇向量连续地映射到另一簇向量
再以键的变形态为例,它的定义如下:

从下面示意图(图6)中我们可以看到一个变形态通过函数的形式将一簇向量不连续地映射到另一簇向量。

图6. 向量态Y将一簇向量连续地映射到另一簇向量
为什么向量态 Y 能将含有向量簇的球形光滑表面映射到一个复杂的可能还不连续的表面呢?我们从上面 Y的定义就可以看出,Y的取值中包含了键的两个端点的位移差。在这种情况下,Y 允许位移场可以是不连续的,虽然位移场不连续,但是原先区域上的每一个点都有位移取值(但是位移的导数不一定存在),所以 Y 就会出现不连续变化的情况。以上我们都是用键的变形态进行举例,因为它的表达式简单比较容易理解,在近场动力学里还有另外一个重要的向量态,即力态。力态是变形态(变形态的值也是向量)的函数。我们将在下一节介绍本构关系时,了解到更多力态的表达式。
在解释了态的基本概念之后,我们大概对向量态,特别是变形态 Y, 有了一个基本的认识。除此之外,我们还需要比较一下传统弹性理论中的能量密度泛函和近场动力学中的能量密度泛函,借此引出另一个数学定义:态的点积。

从上式可以看出,在传统弹性理论中能量密度泛函是应变的“平方”次幂(张量双点积的形式)。那么,我们再来看看下面态基近场动力学模型中的能量密度泛函,值得指出的是,这只是态基近场动力学模型中的一种表达式。

其中 e 是一个标量态,它表达了一根键的伸长量。与传统理论相似,近场动力学模型的能量密度泛函中也含有e 的“平方”次幂。不仅如此,因为在近场动力学理论是非局部理论,即一点与它邻域内关联到该点的所有其他点都有相互作用,所以这一点的能量密度还应该是在该点邻域内积分后所得的值。
为了书写方便,我们将上面这种由态先乘积再积分的形式用如下的粗点积表示,称为态的点积,具体定义如下。(这里需要强调,在此文中我们仅仅解释为“书写方便”,其实我个人认为态的点积在数学理论中有更深刻的意义。但是由于个人的能力有限,加之篇幅有限,不能深入讲解。更多的内容请参阅上面2007年Silling博士发表的文章。)

利用态点积的记号,我们可以重新书写上面的近场动力学的能量密度泛函:
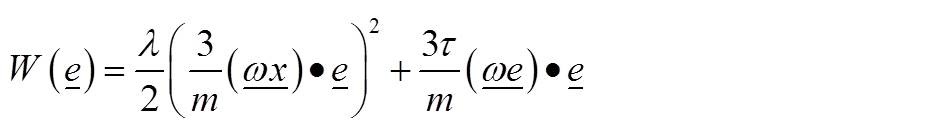
在下一期中,这个能量泛函公式将被用于推导本构关系。届时我们将会有更深入的了解。
值得一提的是,Silling博士等人基于态的点积还定义出了新的广义导数,即所谓的态函数的弗雷歇导数(Fréchet derivative)。应用此导数重新定义了带有积分形式的广义变分。由于篇幅的限制,我们在本文中不展开讲,感兴趣的朋友可以详细阅读原文中的。
本期我们只讲了近场动力学理论里的两个基本的数学概念。目的是为了我们下一讲介绍近场动力学的三种基本本构关系做铺垫。下一讲我们将重点介绍近场动力学模型的本构关系和运动方程,下一讲也是我们这次漫谈的核心内容,敬请期待!
——————————————————————————————————————————————————————
近场动力学(简称PD)理论是国际上刚兴起的基于非局部作用思想建立的一整套力学理论体系,该理论通过求解空间积分方程描述物质力学行为,避免了基于连续性假设建模和求解空间微分方程的传统宏观方法在面临不连续问题时的奇异性[1],所以特别适用于模拟材料的损伤和断裂过程。然而,因为PD模型的数学理论较深,且新概念多用英文表述,所以很多朋友在学习时会遇到一些困难。在朋友的启发下,我想到在微信上建立此公众号,希望将研究PD理论的朋友们聚集起来,分享PD研习路上的点点滴滴,一起解决各自的难题,共同推动PD理论的发展!
[1] 黄 丹, 章 青, 乔丕忠, 沈 峰, 近场动力学方法及其应用. 力学进展, 2010. 40(4): p. 448-459.
每期文章评述的首发平台是微信公众号:近场动力学PD讨论班
也可以搜索微信号:peridynamics
或扫如下二维码加入公众号:

https://blog.sciencenet.cn/blog-232936-1037437.html
上一篇:中国力学大会-2017暨庆祝中国力学学会成立60周年大会 研讨会征稿
下一篇:(力学领域研究热点)近场动力学漫谈(中):本构关系与运动方程