博文
10. 3维空间的各种物理矢量
||
10. 3维空间的各种物理矢量
距离(或位置、长度):
r[1线矢]=r(3)[1线矢],量纲是:[L]
平直坐标:
=x[x基矢]+y[y基矢]+z[z基矢]
={rj[j基矢],j=1到3求和}
曲线坐标:
=rcosθ[x基矢]+rsinθcosφ[y基矢]+rsinθsinφ[z基矢]
=r(3)cosθ[1基矢]+r(3)sinθcosφ[2基矢]
+r(3)sinθsinφ[3基矢],
距离(或位置、长度)的微分:量纲是:[L]
dr[1线矢]=dr(3)[1线矢]
平直坐标:
=dx[x基矢]+dy[y基矢]+dz[z基矢]
={drj[j基矢],j=1到3求和}
曲线坐标:
=d(r(3)cosθ)[x基矢]+d(r(3)sinθcosφ)[y基矢]
+d(r(3)sinθsinφ)[z基矢]
= (dr(3)cosθ+r(3)sinθdθ)[x基矢]
+(dr(3)sinθcosφ+r(3)cosθcosφdθ+r(3)sinθsinφdφ)[y基矢]
+(dr(3)sinθsinφ+r(3)sinθcosφdθ+r(3)sinθcosφdφ)[z基矢],
其模长:量纲是:[L]
r(3)=(rj^2,j=1到3求和)^(1/2),
[r(3)单位1线矢]={rj[j基矢],j=1到3求和}/(rj^2,j=1到3求和)^(1/2),
时间的微分:dt,量纲是:[T]
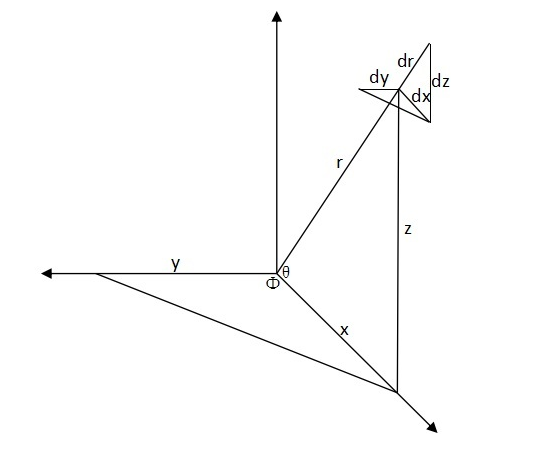
此处φ实为直角=90度。
图1: 3维空间平直坐标与曲线坐标
当φ为直角=90度,则以上有关各式中:cosφ=1,sinφ=0,
当θ为直角=90度,则以上有关各式中:cosθ=1,sinθ=0,
当φ、θ,之一为直角=90度,则3维空间实际上蜕变为2维空间;
当φ、θ,都为直角=90度,则3维空间实际上蜕变为1维空间。
以下各物理量[1线矢],曲线坐标,都类似于r[1线矢]处理的各相应情况。
距离(或位置、长度)的时间导数=速度:量纲是:[L][T]^(-1)
速度v(3)[1线矢]=dr(3)/dt[1线矢]={drj/dt[j基矢],j=1到3求和}
={vj[j基矢],j=1到3求和},
动量=质量乘速度:量纲是:[M][L][T]^(-1)
p(3)[1线矢]=mv(3)[1线矢]=mdr(3)/dt[1线矢]
={mdrj/dt[j基矢],j=1到3求和}
={pj[j基矢],j=1到3求和},
速度的时间导数=加速度:量纲是: [L][T]^(-2)
加速度a(3)[1线矢]=dv(3)/dt[1线矢]={dvj/dt[j基矢],j=1到3求和}
={aj[j基矢],j=1到3求和},
运动力=动量的时间导数:量纲是:[M][L][T]^(-2)
f(3)[1线矢]=dp(3)/dt[1线矢]={d(mvj)/dt[j基矢],j=1到3求和}
={fj[j基矢],j=1到3求和},
偏分[1线矢]={(偏/偏rj)[j基矢],j=1到3求和},量纲是:[L]^(-1)
a(标量)的梯度=梯度a(标量)[1线矢]
={(偏a(标量)/偏rj)[j基矢],j=1到3求和},量纲是:[L]^(-1)
A(3)[1线矢]的散度 =偏分[1线矢]点乘A(3)[1线矢]
={(偏Aj/偏rj),j=1到3求和},量纲是:A(3)的量纲 乘 [L]^(-1)
A(3)[1线矢]的旋度=偏分[1线矢]叉乘A(3)[1线矢]
={(偏Ak/偏rl-偏Al/偏rk)[j基矢],jkl=123循环求和},
量纲是:A(3)的量纲 乘 [L]^(-1)
离心力:
F离心(3)[1线矢]=速度v(3)[1线矢]点乘(偏分r(3)[1线矢]叉乘动量p(3)[1线矢])
={vj(偏pk/偏rl-偏pl/偏rk)[j基矢],jkl=123循环求和},
量纲是:[M][L][T]^(-2)
离心力[1线矢]与运动力[1线矢] 可组成相应的运动方程,其由初始和边界条件确定的解,有各相应能级的周期运动规律。
质量m1距r(3)处引力势(标量):量纲是:[L]^2[T]^(-2)
U=km1/r(3)(标量)
m1、m2距r(3)的引力[1线矢]=m1距r(3)处引力势的梯度乘m2:
量纲是:[M][L][T]^(-2)
f引[1线矢]=((km1/r(3))梯度)m2[1线矢]
=km2{(偏(m1/r(3))/偏rj)[j基矢],j=1到3求和},
k的量纲是:[M]^(-1)[L]^3[T]^(-2),
由引力运动方程,有:
d^2rj/dt^2,j=1到3求和=g=k{(偏(m1/r(3))/偏rj)[j基矢],j=1到3求和},
g是相应条件下,的重力加速度。
其由初始和边界条件确定的解是圆锥曲线(抛物线、椭圆、或双曲线的一支)或其特例(圆或直线)
弹性力:
物体在弹性限度范围内,较小力作用下,弹性力与物体长度成正比:
md^2r(3)/dt^2=kr(3),k为弹性系数。其解为由初始和边界条件确定各相应能级的谐振子。
电荷q1距r(3)处电势[1线矢]
=(q1/r(3))[1线矢]
=q1{rj)[j基矢],j=1到3求和}[1线矢]/r(3),
量纲是:[Q][L]^(-1)=[M]^(1/2)[L]^(1/2)[T]^(-1)
电荷q的量纲[Q]=[M]^(1/2)[L]^(3/2)[T]^(-1)
距q1r(3) 处,电荷q2的静电力[1线矢]
=(q1q2/r(3)^2)[1线矢]
=q1q2{rj[j基矢],j=1到3求和}/r(3)^2,量纲是:[M][L] [T]^(-2),
q1距r(3)处的电场强度[1线矢]:
E(3)[1线矢]={(偏(q1rj/r(3))/偏(ict)-偏(ig0/r(3))/偏(rj))[j基矢],j=1到3求和},量纲是:[M]^(1/2)[L]^(-3/2)[T]^(-1),
q1距r(3)处的磁场强度[1线矢]
=H(3)[1线矢]
=偏分r(3)[1线矢]叉乘(q1/r(3))[1线矢]
={(偏/偏rj)[j基矢],j=1到3求和}叉乘
q1{rj/r(3) [j基矢],j=1到3求和}
=q1{(偏(rk/r(3))/偏((rl)-偏(rl/r(3))/偏(rk))[j基矢]
,j=1到3求和},量纲是:[M]^(1/2)[L]^(-3/2)[T]^(-1),
距q1r(3) 处,电荷q2的磁力[1线矢]
=q2 v(3)H(3)[1线矢]
=q1 q2 v(3){(偏(rk/r(3))/偏((rl)-偏(rl/r(3))/偏(rk))[j基矢]
,j=1到3求和},量纲是:[M][L] [T]^(-2),
q1、q2距r的电力[1线矢]、磁力[1线矢],量纲都是: [M][L][T]^(-2),
其中,[M]表明:“电、磁”也有“质量”的量纲。
静电力[1线矢]、磁力[1线矢],都可与运动力[1线矢]组成相应的运动方程,其由初始和边界条件确定的解,也有各相应能级的周期运动规律。
还发展得到:E(3)和H(3)随时间和空间变化的马克斯威尔方程组和达仑贝尔方程等电动力学方程。
对于各种矢量,都只是在坐标中心处的,根本不存在什么“传播速度”、“瞬时传播”的问题。
(未完待续)
https://blog.sciencenet.cn/blog-226-1149012.html
上一篇:特别代表王毅带队!中印边界谈判首次提到“一线部队”!
下一篇:科学认识、运用客观世界的基本特性(5)