博文

数学笔记

已有 3714 次阅读 2017-4-29 16:56 |个人分类:知识|系统分类:科研笔记| 数学, 名词

diffeomorphism 微分同胚
https://en.wikipedia.org/wiki/Diffeomorphism

http://mathworld.wolfram.com/Diffeomorphism.html
A diffeomorphism is a map between manifolds which is differentiable and has a differentiable inverse.

--------------------------------------------------------------------------------------------------------------

isomorphism 同构
https://en.wikipedia.org/wiki/Isomorphism

http://mathworld.wolfram.com/Isomorphism.html

Isomorphism is a very general concept that appears in several areas of mathematics. The word derives from the Greek iso, meaning "equal," and morphosis, meaning "to form" or "to shape."

Formally, an isomorphism is bijective morphism. Informally, an isomorphism is a map that preserves sets and relations among elements. " is isomorphic to " is written . Unfortunately, this symbol is also used to denote geometric congruence.

An isomorphism from a set of elements onto itself is called an automorphism.

--------------------------------------------------------------------------------------------------------------
morphism 态射

http://mathworld.wolfram.com/Morphism.html
A morphism is a map between two objects in an abstract category.

--------------------------------------------------------------------------------------------------------------
homomorphism 同态

http://mathworld.wolfram.com/Homomorphism.html
A term used in category theory to mean a general morphism. The term derives from the Greek (omo) "alike" and (morphosis), "to form" or "to shape." The similarity in meaning and form of the words "homomorphism" and "homeomorphism" is unfortunate and a common source of confusion.

--------------------------------------------------------------------------------------------------------------

homeomorphism 同胚

http://mathworld.wolfram.com/Homeomorphism.html

A homeomorphism, also called a continuous transformation, is an equivalence relation and one-to-one correspondence between points in two geometric figures or topological spaces that is continuous in both directions. A homeomorphism which also preserves distances is called an isometry. Affine transformations are another type of common geometric homeomorphism.

The similarity in meaning and form of the words "homomorphism"and "homeomorphism" is unfortunate and a common source of confusion.

--------------------------------------------------------------------------------------------------------------

monomorphism 单射

http://mathworld.wolfram.com/Monomorphism.html
A morphism in a category is a monomorphism if, for any two morphisms, implies that . In the categories of sets, groups, modules, etc., a monomorphism is the same as an injection, and is used synonymously with "injection" outside of category theory.

--------------------------------------------------------------------------------------------------------------

epimorphism(surjection) 满射

http://mathworld.wolfram.com/Epimorphism.html
A morphism in a category is an epimorphism if, for any two morphisms , implies . In the categories of sets, groups, modules, etc., an epimorphism is the same as a surjection, and is used synonymously with "surjection" outside of category theory.

--------------------------------------------------------------------------------------------------------------

category 范畴

http://mathworld.wolfram.com/Category.html
A category consists of three things: a collection of objects, for each pair of objects a collection of morphisms (sometimes call "arrows") from one to another, and a binary operation defined on compatible pairs of morphisms called composition. The category must satisfy an identity axiom and an associative axiom which is analogous to the monoid axioms.

The morphisms must obey the following laws:

1. If is a morphism from to (in short, ), and , then there is a morphism (commonly read " composed with ") from to .

2. Composition of morphisms, where defined, is associative, so if , , and , then .

3. For each object a, there is an identity morphism , such that for any , and .

In most concrete categories over sets, an object is some mathematical structure (e.g., a group, vector space, or smooth manifold) and a morphism is a map between two objects. The identity map between any object and itself is then the identity morphism, and the composition of morphisms is just function composition.

One usually requires the morphisms to preserve the mathematical structure of the objects. So if the objects are all groups, a good choice for a morphism would be a group homomorphism. Similarly, for vector spaces, one would choose linear maps, and for differentiable manifolds, one would choose differentiable maps.

In the category of topological spaces, morphisms are usually continuous maps between topological spaces. However, there are also other category structures having topological spaces as objects, but they are not nearly as important as the "standard" category of topological spaces and continuous maps.

--------------------------------------------------------------------------------------------------------------

isometry 等距同构

http://mathworld.wolfram.com/Isometry.html
A bijective map between twometric spaces that preserves distances, i.e.,

where is the map and is the distance function. Isometries are sometimes also called congruence transformations. Two figures that can be transformed into each other by an isometry are said to be congruent (Coxeter and Greitzer 1967, p. 80).

An isometry of the plane is a linear transformation which preserves length. Isometries include rotation, translation, reflection, glides, and the identity map. Two geometric figures related by an isometry are said to be geometrically congruent (Coxeter and Greitzer 1967, p. 80).

If a plane isometry has more than one fixed point, it must be either the identity transformation or a reflection. Every isometry of period two (two applications of the transformation preserving lengths in the original configuration) is either a reflection or a half-turn rotation. Every isometry in the plane is the product of at most three reflections (at most two if there is a fixed point). Every finite group of isometries has at least one fixed point.

--------------------------------------------------------------------------------------------------------------

--------------------------------------------------------------------------------------------------------------

manifold 流形

http://mathworld.wolfram.com/Manifold.html
A manifold is a topological space that is locally Euclidean (i.e., around every point, there is a neighborhood that is topologically the same as the open unit ball in ). To illustrate this idea, consider the ancient belief that the Earth was flat as contrasted with the modern evidence that it is round. The discrepancy arises essentially from the fact that on the small scales that we see, the Earth does indeed look flat. In general, any object that is nearly "flat" on small scales is a manifold, and so manifolds constitute a generalization of objects we could live on in which we would encounter the round/flat Earth problem, as first codified by Poincaré.

More concisely, any object that can be "charted" is a manifold.

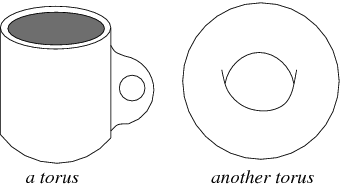
One of the goals of topology is to find ways of distinguishing manifolds. For instance, a circle is topologically the same as any closed loop, no matter how different these two manifolds may appear. Similarly, the surface of a coffee mug with a handle is topologically the same as the surface of the donut, and this type of surface is called a (one-handled) torus.

As a topological space, a manifold can be compact or noncompact, and connected or disconnected. Commonly, the unqualified term "manifold"is used to mean "manifold with boundary." This is the usage followed in this work. However, an author will sometimes be more precise and use the term open manifold for a noncompact manifold without boundary or closed manifold for a compact manifold with boundary.

If a manifold contains its own boundary, it is called, not surprisingly, a "manifold with boundary." The closed unit ball in is a manifold with boundary, and its boundary is the unit sphere. The concept can be generalized to manifolds with corners. By definition, every point on a manifold has a neighborhood together with a homeomorphism of that neighborhood with an open ball in . In addition, a manifold must have a second countable topology. Unless otherwise indicated, a manifold is assumed to have finite dimension, for a positive integer.

Smooth manifolds (also called differentiable manifolds) are manifolds for which overlapping charts "relate smoothly" to each other, meaning that the inverse of one followed by the other is an infinitely differentiable map from Euclidean space to itself. Manifolds arise naturally in a variety of mathematical and physical applications as "global objects." For example, in order to precisely describe all the configurations of a robot arm or all the possible positions and momenta of a rocket, an object is needed to store all of these parameters. The objects that crop up are manifolds. From the geometric perspective, manifolds represent the profound idea having to do with global versus local properties.

The basic example of a manifold is Euclidean space, and many of its properties carry over to manifolds. In addition, any smooth boundary of a subset of Euclidean space, like the circle or the sphere, is a manifold. Manifolds are therefore of interest in the study of geometry, topology, and analysis.

A submanifold is a subset of a manifold that is itself a manifold, but has smaller dimension. For example, the equator of a sphere is a submanifold. Many common examples of manifolds are submanifolds of Euclidean space. In fact, Whitney showed in the 1930s that any manifold can be embedded in , where .

A manifold may be endowed with more structure than a locally Euclidean topology. For example, it could be smooth, complex, or even algebraic (in order of specificity). A smooth manifold with a metric is called a Riemannian manifold, and one with a symplectic structure is called a symplectic manifold. Finally, a complex manifold with a Kähler structure is called a Kähler manifold.

--------------------------------------------------------------------------------------------------------------

topological space 拓扑空间

http://mathworld.wolfram.com/TopologicalSpace.html
A topological space, also called an abstract topological space, is a set

together with a collection of open subsets

that satisfies the four conditions:

1. The empty set is in .

2. is in .

3. The intersection of a finite number of sets in is also in .

4. The union of an arbitrary number of sets in is also in .

Alternatively, may be defined to be the closed sets rather than the open sets, in which case conditions 3 and 4 become:

3. The intersection of an arbitrary number of sets in is also in .

4. The union of a finite number of sets in is also in .

These axioms are designed so that the traditional definitions of open and closed intervals of the real line continue to be true. For example, the restriction in (3) can be seen to be necessary by considering $intersection _(n=1)^infty(-1/n,1/n)={0}$ , where an infinite intersection of open intervals is a closed set.

In the chapter "Point Sets in General Spaces" Hausdorff (1914) defined his concept of a topological space based on the four Hausdorff axioms (which in modern times are not considered necessary in the definition of a topological space).

--------------------------------------------------------------------------------------------------------------

holomophic function 全纯函数

http://mathworld.wolfram.com/HolomorphicFunction.html
A synonym for analytic function, regular function, differentiable function, complex differentiable function, and holomorphic map (Krantz 1999, p. 16). The word derives from the Greek

(holos), meaning "whole," and

(morphe), meaning "form" or "appearance."

Many mathematicians prefer the term "holomorphic function" (or "holomorphic map") to "analytic function" (Krantz 1999, p. 16), while "analytic" appears to be in widespread use among physicists, engineers, and in some older texts (Morse and Feshbach 1953, pp. 356-374; Knopp 1996, pp. 83-111; Whittaker and Watson 1990, p. 83).

--------------------------------------------------------------------------------------------------------------

moniod 幺半群

http://mathworld.wolfram.com/Monoid.html
A monoid is a set that is closed under an associative binary operation and has an identity element

such that for all

. Note that unlike a group, its elements need not have inverses. It can also be thought of as a semigroup with an identity element.

A monoid must contain at least one element.

A monoid that is commutative is, not surprisingly, known as a commutativemonoid.

--------------------------------------------------------------------------------------------------------------

normal subgroup 正规子群

http://mathworld.wolfram.com/NormalSubgroup.html
Let

be a subgroup of a group

. The similarity transformation of

by a fixed element

not in

always gives a subgroup. If

for every element in , then is said to be a normal subgroup of , written (Arfken 1985, p. 242; Scott 1987, p. 25). Normal subgroups are also known as invariant subgroups or self-conjugate subgroup (Arfken 1985, p. 242).