博文
【FOP Outstanding Paper】 瑞利-泰勒不稳定性演化过程中的粘性、热传导和Prandtl数效应
|
中国物理学界年度盛会—物理学会秋季会议于9月19日在郑州大学开幕。9月20日,中国物理学会组织了中国物理学期刊专场报告会暨优秀论文颁奖活动。Frontiers of Physics今年为13篇优秀论文颁发“Outstanding Paper Awards 2019”证书。
北京应用物理与计算数学研究所许爱国课题组与山东交通学院航空学院陈锋课题组合作发表的一篇论文获此奖项:Feng Chen, Ai-Guo Xu, and Guang-Cai Zhang, Viscosity, heat conductivity, and Prandtl number effects in the Rayleigh–Taylor Instability, Front. Phys. 11(6), 114703 (2016)
FOP Outstanding Paper
Rayleigh–Taylor不稳定性演化过程中的粘性、热传导和Prandtl数效应
当重流体处于轻流体上方时,如果界面无限平整且不存在扰动,则该流体系统处于不稳定平衡状态。由于在自然界中扰动的不可避免性,即便是原本无限平整的界面在重力作用下也会发生失稳。这种由于轻流体推重流体(逆着加速度方向)或加速度由重流体指向轻流体所导致的流体界面不稳定性现象,一般称为瑞利泰勒不稳定性 (Rayleigh–Taylor Instability,RTI)现象。其中,轻流体在重流体中往前推进时,由于自身“材料强度”比周围重流体“材料强度”低,所以头部容易“变钝”而逐渐发展成“气泡”状;而重流体在轻流体中推进时则由于其自身“材料强度”比周围的轻流体“材料强度”高而相对不易变形而逐渐发展成“尖钉”状。这种不稳定性在一些自然现象(例如天文现象)和工业领域(例如惯性约束聚变、内燃机燃烧等)中都扮演了重要角色:在惯性约束聚变内爆过程的减速阶段,RTI会影响靶丸的均匀压缩,严重情况下会导致靶丸壳层的破裂;同时在点火阶段中,RTI还会引起壳层材料与热区的掺混,降低中心热区的温度,导致点火失败。作为一种满足条件就会发生的物理现象,它在惯性约束聚变等类似过程中带来的效应是不利的;但在与一些内燃机燃烧推进相关的过程中,它的存在与演化会进一步引发开尔文–亥姆霍兹(界面)不稳定性(Kelvin–Helmhltz Instability, KHI),RTI与KHI合在一起,共同加剧液体燃料与氧气的混合,对于促进燃烧过程是有利的。另外,在天体物理中的超新星爆发等过程中,也会出现RTI现象。人们在生活和工业生产中对RTI的处置原则,自然是有利则强之,有害则抑之。精准、有效地强化和抑制的前提是对其发生、发展各个阶段的特征、机制和规律有个清晰的认识。因此RTI研究具有重要的学术意义和潜在的工程应用需求。

图1 Rayleigh–Taylor 卷云[Y. Zhou, Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing (I), Physics Reports 720, 1 (2017)].
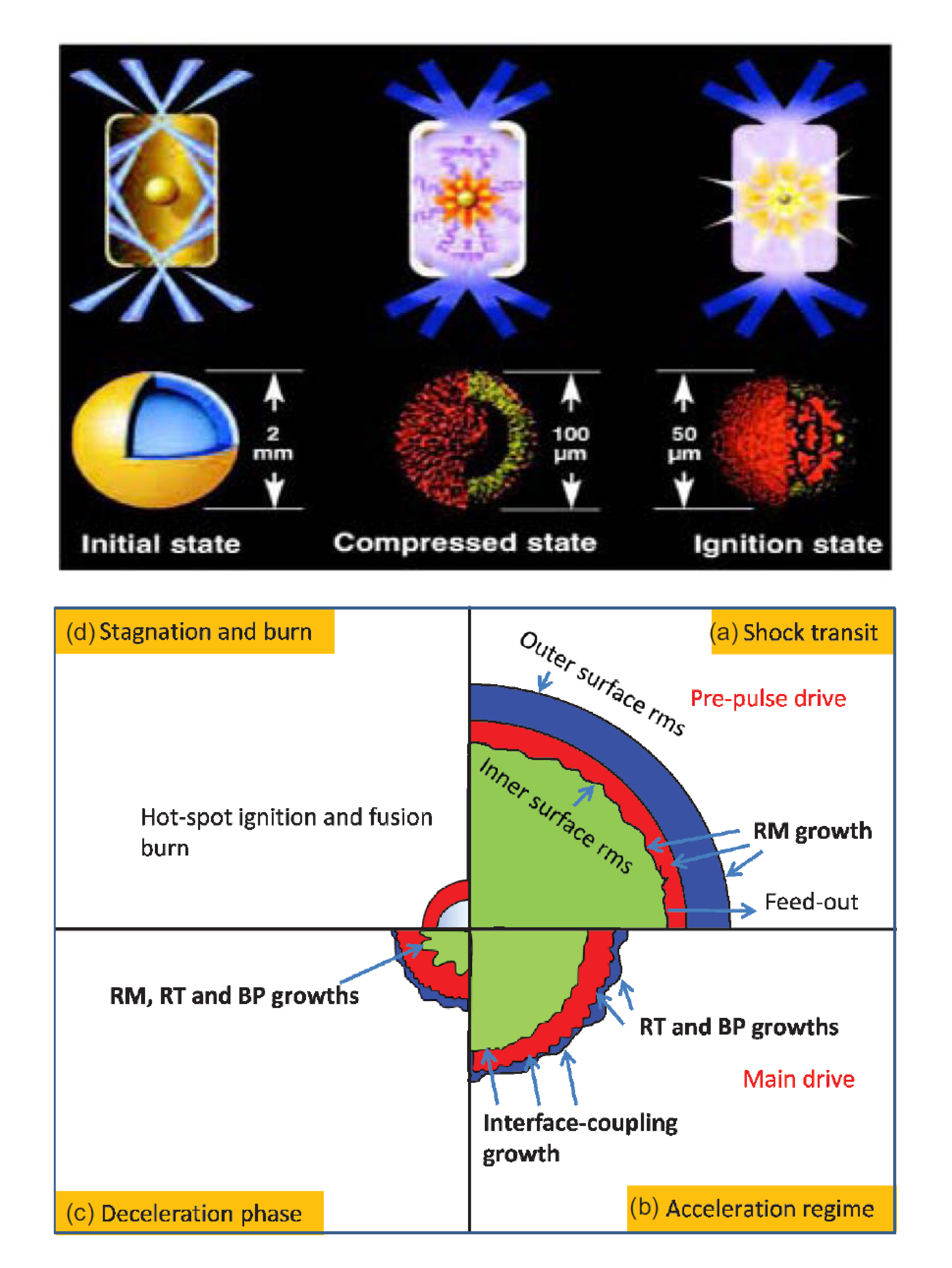
图2 惯性约束聚变中易遭遇Rayleigh–Taylor不稳定性[下图来自文献:L. F. Wang, et al., Sci. China-Phys. Mech. Astron. 60, 055201 (2017)].

图3 燃烧过程中流体不稳定性促进燃料与氧气的充分混合[百度图库火焰燃烧视频素材:http://image.baidu.com/search/index?tn=baiduimage&ps=1&ct=201326592&lm=-1&cl=2&nc=1&ie=utf-8&word=%E7%87%83%E7%83%A7].
这些系统具有如下特点:其本身可能是宏观尺度的,但其内部存在大量的中间尺度的空间结构和动理学模式;这些结构和模式的存在与演化极大地影响着系统的物理性能和功能。这类系统内部往往具有大量的界面,包括物质界面和力学界面(冲击波、爆轰波、边界层等),系统内部的受力和响应过程非常复杂。
RTI模拟研究,尽管进行了这么多年,取得了如此多的进展,但问题本身的复杂性和认知发展的阶段性决定了我们现阶段的研究仍然面临如下两方面的挑战:第一是如何模拟:如何把系统存在的、我们感兴趣的结构和过程客观地模拟出来?第二是如何把握:数值模拟给出的是海量数据、复杂物理场,信息量极大,如何将其中更多的特征、机制和规律提取出来?模拟方法、分析方法的局限性决定了我们目前获得的认知相对于系统本身的复杂性而言,仍然是少得可怜,绝大多数信息仍然处于沉睡和待认知状态。
与如何模拟相关的注意事项(至少)包括:数值模拟是以在相应的尺度上物理模型有效和具备所需功能为前提的;网格大小和时间步长是以物理模型的最小有效尺度为下限的;物理建模层面的误差是无法通过算法精度提高来弥补的。就RTI演化系统而言,其中的大尺度缓变行为可以使用Navier–Stokes(NS)方程很好地描述,但在一些小结构和快模式描述方面,基于连续介质假设和只考虑一阶非平衡效应的NS描述受到挑战;即便是在NS有效的情形,作为一种粗粒化物理建模,其在具体非平衡状态和行为描述方面也可能无法满足需求。
与如何把握相关的注意事项(至少)包括:复杂流动过程中涉及各种复杂的非平衡行为。这些非平衡行为的复杂性(横看成岭侧成峰,远近高低各不同)决定了非平衡状态和程度描述所需要的多角度性。Knudsen数、 粘性、 热传导、 (密度、流速、温度、压强等)宏观量的梯度等都是常用的非平衡程度表征量,它们都从各自的角度来描述系统的非平衡程度。但它们也都是将某些信息高度浓缩的、平均化粗粒描述,很多关于非平衡状态的具体信息(例如,不同自由度上的内能、高阶非守恒矩的具体数值以及它们各独立分量的具体搭配等),通过它们是看不到、无法直接研究的。因而,除此之外,我们还需要更加细粒化的描述。需要指出的是,在细粒化描述方面,微观分子动力学描述虽然理想但却往往因为适用的时间空间尺度受限而无能为力。
离散Boltzmann方法/模型(Discrete Boltzmann Method/Model, DBM)就是针对上述物理描述的背景需求发展起来的介观建模方法和分析方法/模型[1],其思想最初起源于2012年发表在Frontiers of Physics的一篇综述文献[2]。从效果上看,离散Boltzmann模型相当于一个宏观流体模型外加一个关于热动非平衡效应的粗粒化模型。该宏观流体模型可以是Navier-Stokes,也可以超越Navier-Stokes。该粗粒化模型(后者)可用于弥补宏观流体模型(前者)在具体非平衡状态或效应描述方面的不足,其目的在于帮助理解、进而改进宏观流体模型中的线性或非线性本构关系。在物理描述精细程度方面,DBM比原始Boltzmann方程粗粒化,但比Navier–Stokes方程组细粒化,介于二者之间;在适用的时空尺度方面,超越微观的分子动力学模拟。所以,作为宏观流体描述和微观分子动力学描述的桥梁和有益补充,DBM为复杂流体系统主要非平衡行为特征的研究提供了一套全新、便捷、有效的思路和方法。
在非平衡状态和行为特征更精细描述方面,DBM中(f - f eq )的非守恒动理学矩可满足或部分满足上述需求(f 是分布函数, f eq是与f对应的热力学平衡态分布函数)。除了可以通过这些非平衡矩研究系统的熵增,进而通过熵增研究物质混合,研究系统内不同非平衡行为特征之间的空间关联、时间关联、时空关联、竞争与协作等之外,借助非平衡量相空间到原点距离的概念又可定义高度粗粒化的非平衡程度或强度;借助非平衡量相空间两点间距离的概念可以定义两个非平衡状态之间的相似度(两点间距离的倒数);如果这两个状态都随时间演化,那么我们计算在某段时间内两点间距离的平均值,通过其倒数定义这两个动理学过程之间的相似度,等等。这些描述相互相成,构成对流体系统非平衡状态和行为的相对完备描述。
DBM看重的是其在非平衡行为描述方面超越Navier–Stokes等宏观流体模型的物理功能,建模过程要保的是物理问题研究所依赖的物理量、基本的守恒性、必要的对称性等。DBM可以根据需要研究的非平衡程度和选定研究的具体非平衡行为特征来“有所保,有所丢”,通过抓主要矛盾来构建满足需求的最精简形式。因为物理模型的描述能力从某个角度提升一步,就会带来大量新的物理问题需要研究,所以目前基于DBM的复杂流动研究采取分步走策略:第一步是基于只考虑一阶热力学非平衡效应构建DBM,除了NS可以描述的流体行为,重点关注NS遗漏的非平衡行为特征(例如,驱动与响应、各类关联、粘性/热传导/Prandtl数/马赫数等对上述效应和关联的影响等);然后逐步考虑更高阶次非平衡效应[1–5]。在基于DBM的模拟研究中,一般包含两部分内容:一部分是传统流体模型NS也可以给出的,一部分是NS所不能给出的。这两部分内容相互相成,构成对流体系统的一个更加完备的描述。
本文使用课题组发展的多弛豫时间(Multiple Relaxation Time, MRT) DBM从宏观和非平衡特征两个角度研究Rayleigh-Taylor不稳定性问题,尤其探讨了(1)系统内密度、流速、温度、压强等宏观量的不均匀度与各种不同形式的非平衡行为之间的关联度,(2)粘性、热传导、Prandtl数对界面扰动增长过程、对上述各类关联的影响。相对于单弛豫时间DBM,在MRT-DBM中,不同非守恒动理学矩的弛豫时间可以相对独立地调节,因而Prandtl数不再固定为常数。模拟发现,(1)粘性和热传导(进而Prandtl数)效应非常丰富、复杂,但又有规律可循:它们对界面扰动幅度增长、对各类非平衡行为之间关联度的影响均表现出阶段性,但涉及到的阶段却可能是从不同角度去划分的。(2)粘性和热传导对界面扰动幅度增长速率的影响表现出阶段性:在进入再加速阶段以前,二者的影响较小;进入再加速阶段后,二者均表现显著的抑制作用,且Pr数效应不单调(如图4所示);粘性、热传导对RT不稳定性的抑制作用主要通过抑制KH不稳定性的发展来实现(如图5所示)。(3)远离界面的地方,密度不均匀度和热力学非平衡强度均近似为0;两者的特征一致性较高(如图6所示)。(4)密度不均匀度和全局平均非平衡强度之间、温度不均匀度和全局平均无组织能量流强度之间都存在相当高的相关度,近似为1;速度不均匀度和全局平均无组织动量流强度之间的相关度也相对较高(如图7所示)。(5)粘性和热传导对上述前两组特征之间(密度不均匀度和全局平均非平衡强度之间、温度不均匀度和全局平均无组织能量流强度之间)的相关度有影响,且粘性和热传导二者的影响表现出不同的特征。(6)就密度不均匀度和全局平均非平衡强度之间的相关度而言,在湍流混合阶段之前热传导起主要作用,而粘性的影响主要体现在湍流混合阶段。具体来说,(i)在湍流混合阶段之前,热传导率越大,相关度越高,随着热传导的增加,相关度逐渐趋于1,该趋势可以用热导率的指数衰减函数表示;(ii)进入湍流混合阶段之后,若热导率保持不变,则粘性系数越大,相关度越高(如图8所示)。(7)就温度不均匀度和全局平均无组织能量流之间的相关度而言,在扰动幅度随时间增长的线性阶段热传导效应起主要作用,热传导越强,相关度越高,粘性效应的影响较弱;在扰动幅度随时间的增长进入非线性阶段后,粘性效应开始更加显著(如图9所示)。(8)相关度近似为1的两组非平衡行为特征之间存在(近似)线性关系,热传导影响的是该线性关系的斜率,且这两组线性关系的斜率均随着热传导增大而升高(如图8、9所示)。
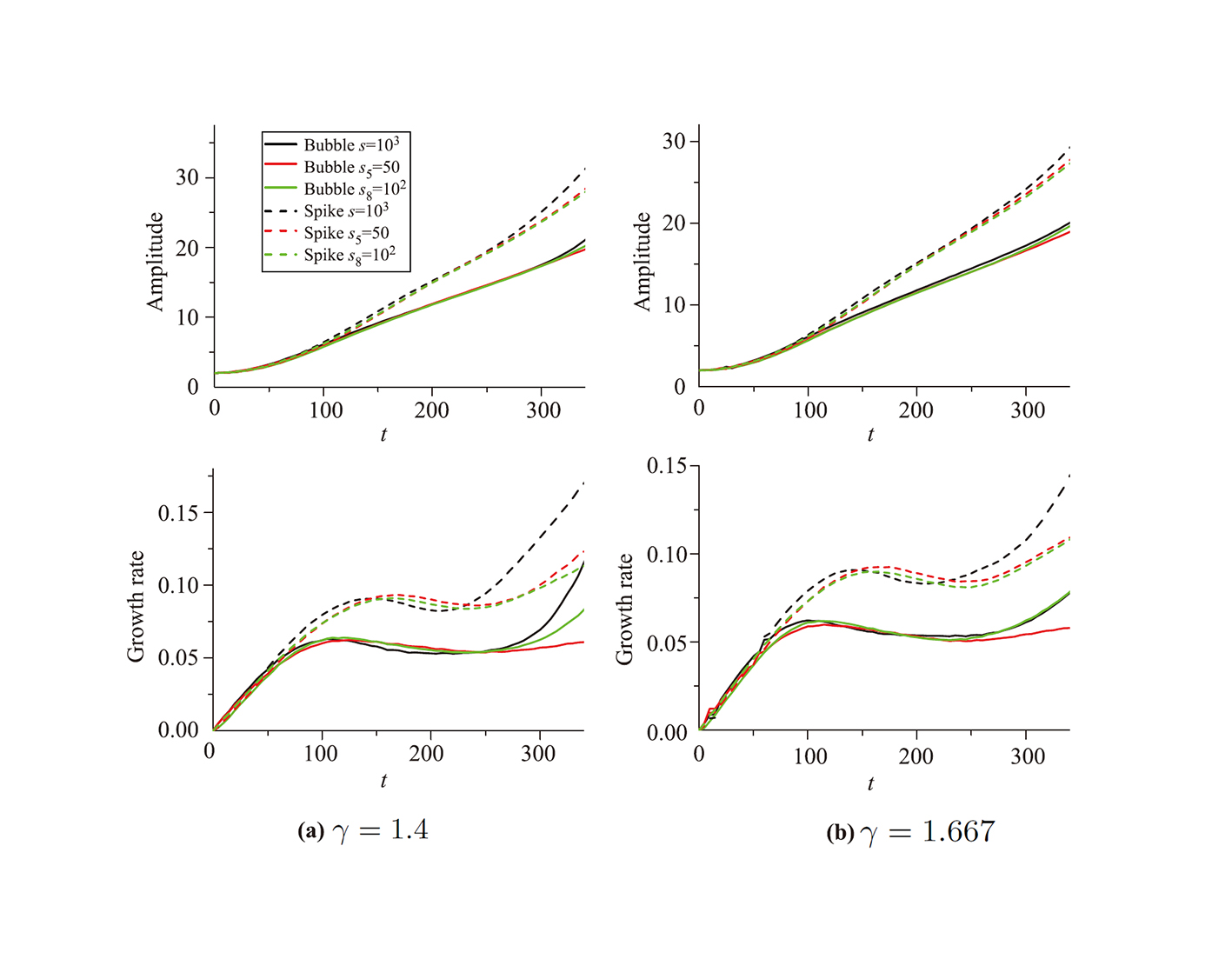
图4 粘性、热传导对气泡、尖钉振幅与增长率的影响.

图5 RT不稳定性的速度矢量图.
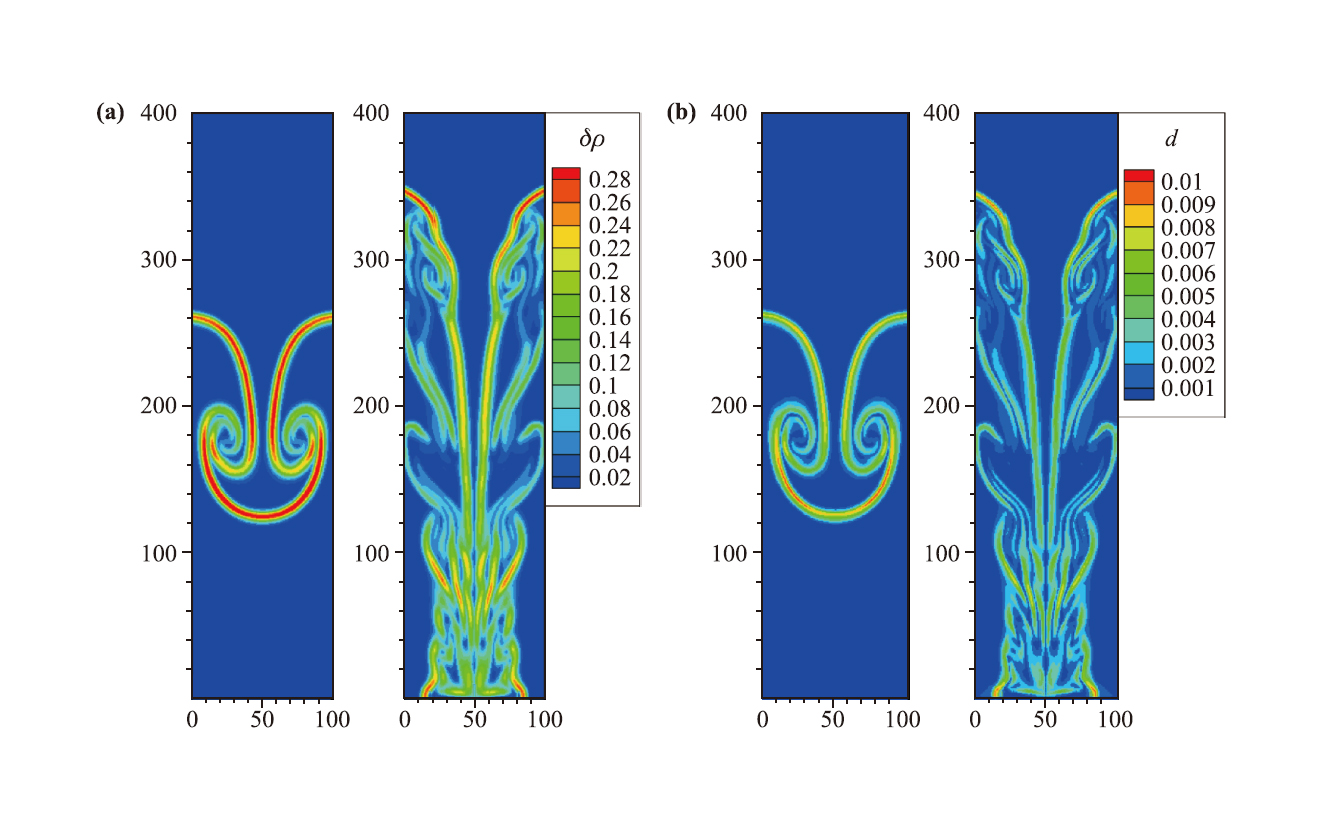
图6 密度不均匀度和热力学非平衡强度在t=200和t=400时的空间分布图. (a)密度不均匀度,(b)热力学非平衡强度.
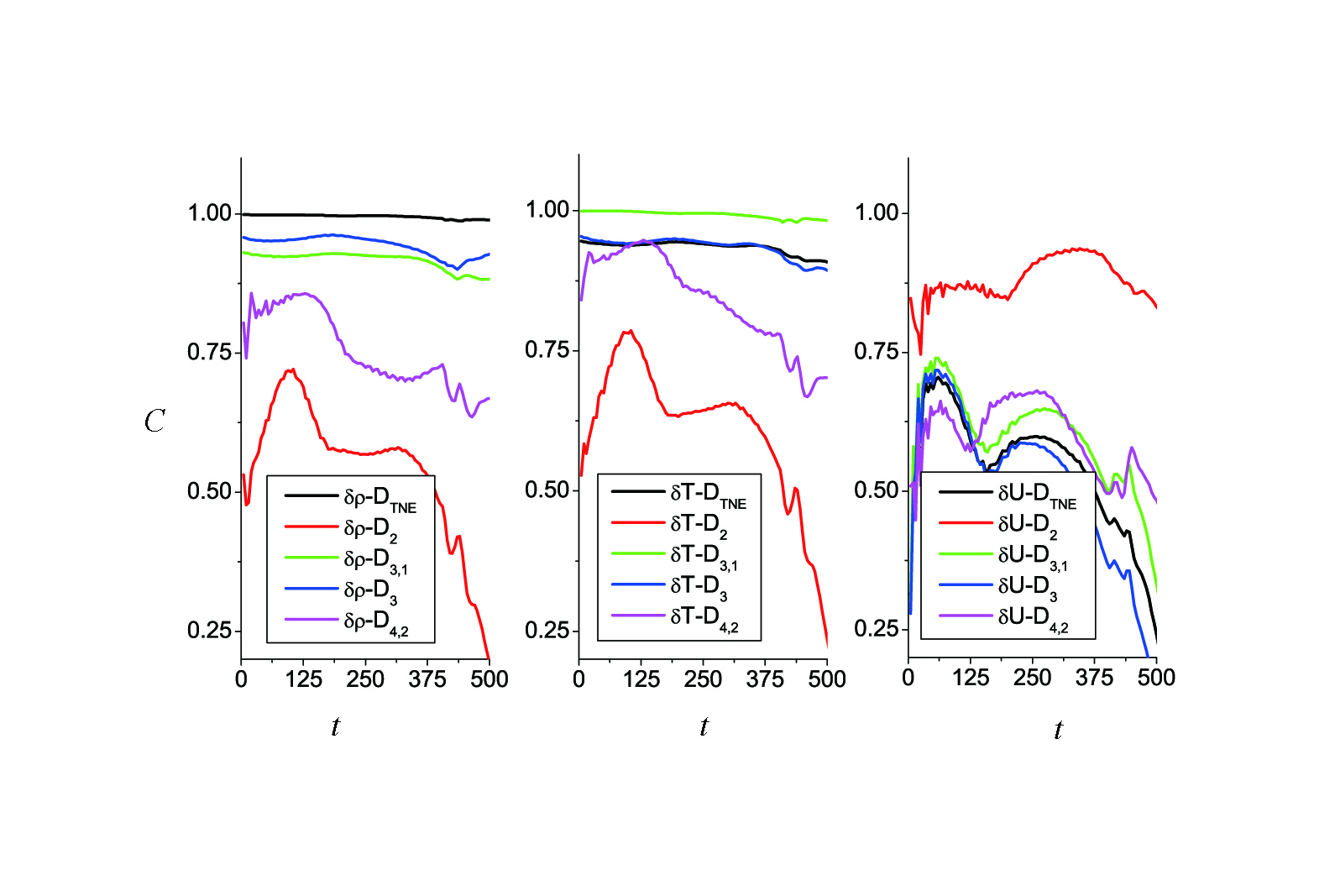
图7 密度、温度、流速不均匀度与各类非平衡强度之间的相关度.
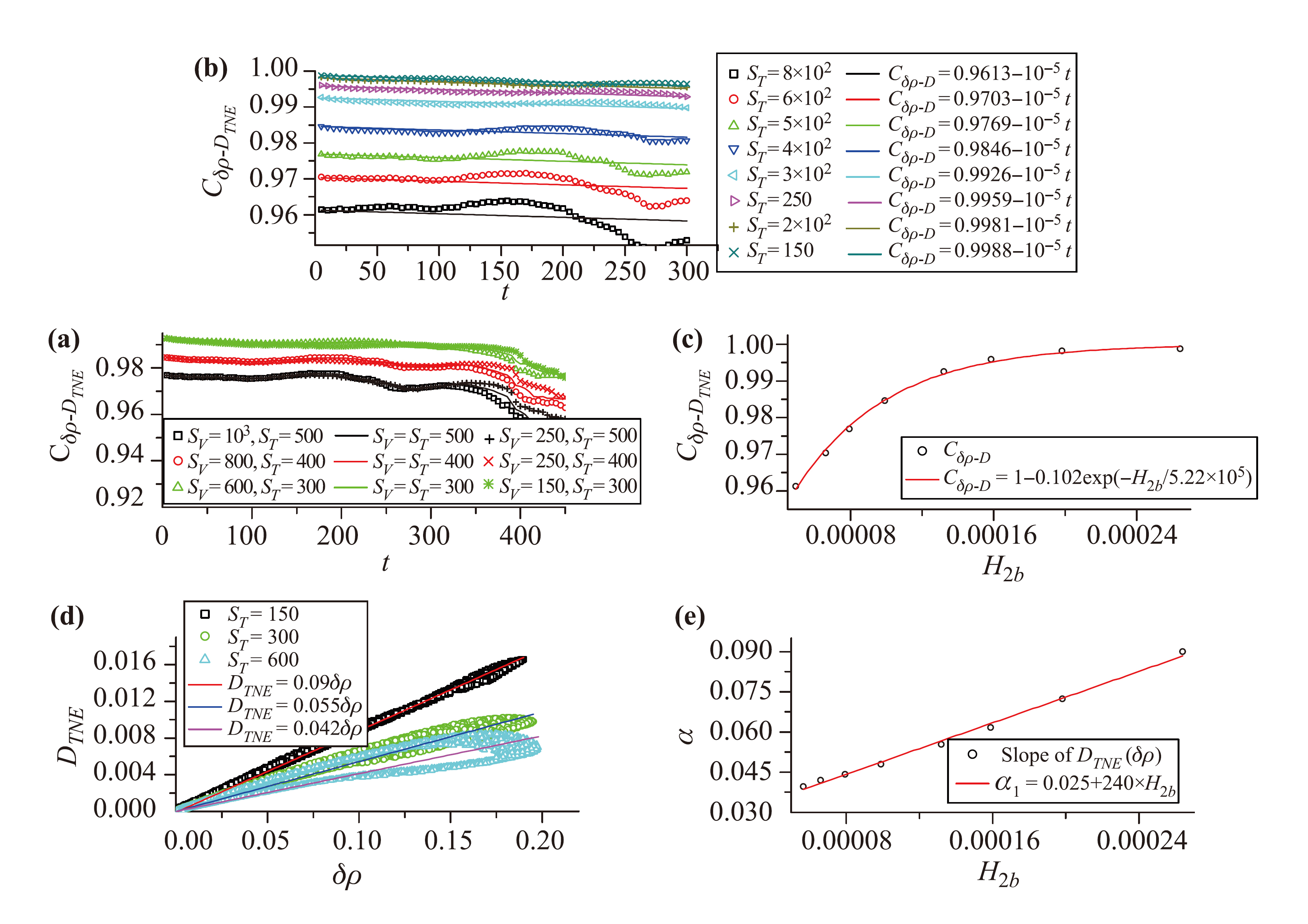
图8 粘性、热传导对密度不均匀度和全局平均非平衡强度之间相关度的影响(H2b是无量纲热传导率).
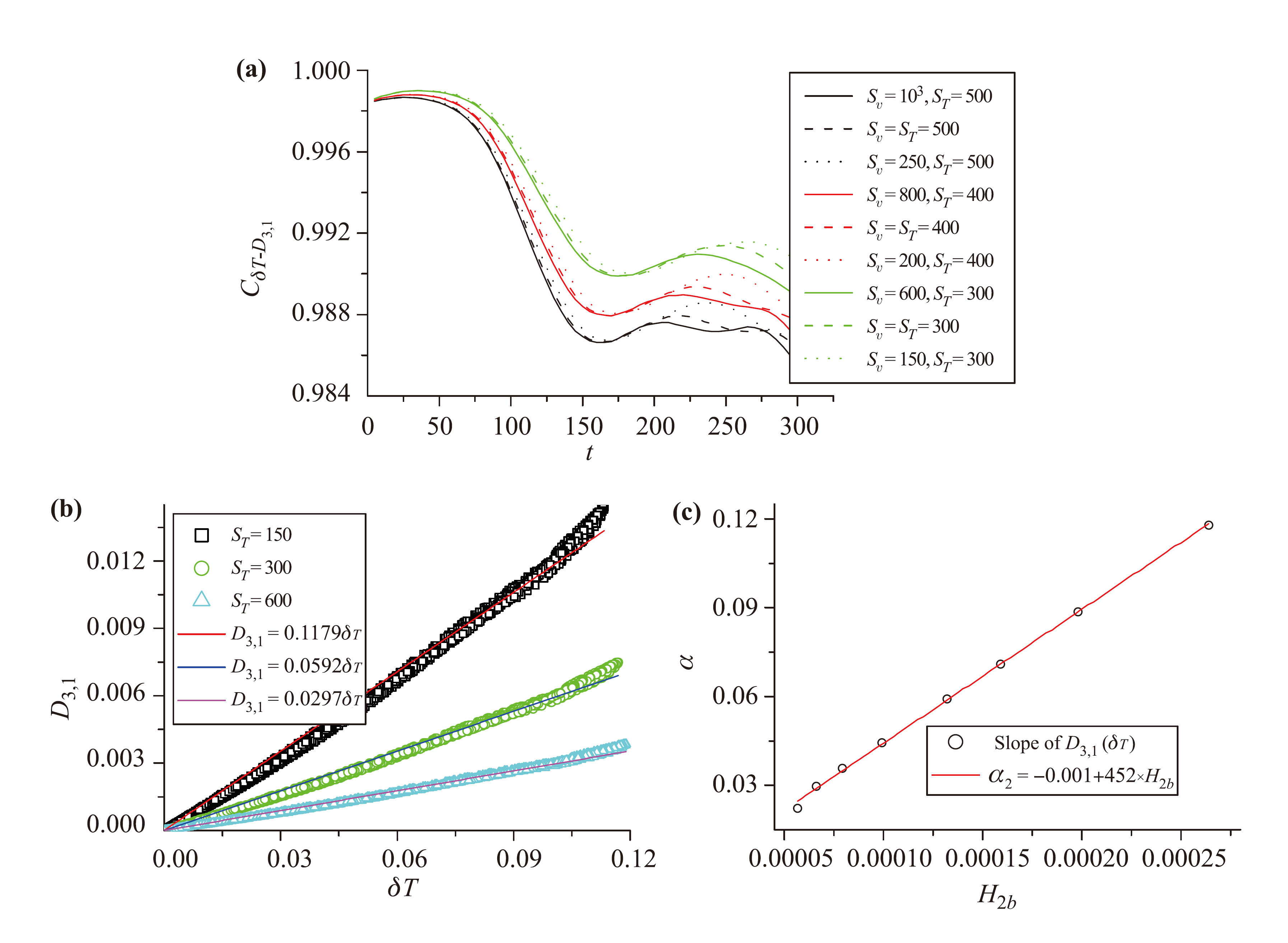
图9 粘性、热传导对温度不均匀度和全局平均无组织能量流强度之间相关度的影响.
更详细的内容请参见原文[6]。 该工作的后续工作之一[7]发表在Physics of Fluids,并被选做Editor’s pick进行推介,详见微信公众号“京师物理”2018-11-08的推文“研究进展:流体不稳定性发展过程中的非平衡行为特征、相关性、竞争与合作”。其他相关研究工作可参见[8–10]。
参考文献
1. Ai-Guo Xu, Guang-Cai Zhang, and Yu-Dong Zhang, Discrete Boltzmann modeling of compressible flows, in: G. Z. Kyzas and A. C. Mitropoulos (Eds.), Kinetic Theory, InTech, Rijeka, 2018, Ch. 02. doi:10.5772/intechopen.70748
2. Ai-Guo Xu, Guang-Cai Zhang, Yan-Biao Gan, Feng Chen, and Xi-Jun Yu, Lattice Boltzmann modeling and simulation of compressible flows, Frontiers of Physics 7, 582 (2012)
3. Yan-Biao Gan, Ai-Guo Xu, Guang-Cai Zhang, Yu-Dong Zhang, and Sauro Succi, Discrete Boltzmann trans-scale modeling of high-speed compressible flows, Physical Review E 97,053312 (2018)
4. Yu-Dong Zhang, Ai-Guo Xu, Guang-Cai Zhang, Zhi-Hua Chen, and Pei Wang, Discrete ellipsoidal statistical BGK model and Burnett equations, Frontiers of Physics 13(3), 135101 (2018)
5. Yu-Dong Zhang, Ai-Guo Xu, Guang-Cai Zhang, and Zhi-Hua Chen, Discrete Boltzmann method for non-equilibrium flows: Based on Shakhov model, Computer Physics Communications 238, 50 (2019)
6. Feng Chen, Ai-Guo Xu, and Guang-Cai Zhang, Viscosity, heat conductivity, and Prandtl number effects in the Rayleigh–Taylor Instability, Frontiers of Physics 11, 114703 (2016)
7. Feng Chen, Ai-Guo Xu, and Guang-Cai Zhang, Collaboration and competition between Richtmyer–Meshkov instability and Rayleigh–Taylor instability, Physics of Fluids 30, 102105 (2018)
8. Hui-Lin Lai, Ai-Guo Xu, Guang-Cai Zhang, Yan-Biao Gan, Yang-Jun Ying, and Sauro Succi, Nonequilibrium thermohydrodynamic effects on the Rayleigh–Taylor instability in compressible flows, Physical Review E 94, 023106 (2016)
9. Chuan-Dong Lin, Ai-Guo Xu, Guang-Cai Zhang, Kai-Hong Luo, and Ying-Jun Li, Discrete Boltzmann modeling of Rayleigh–Taylor instability in two-component compressible flows, Physical Review E 96, 053305 (2017)
10. 李德梅, 赖惠林, 许爱国, 张广财, 林传栋, 甘延标. 可压流体Rayleigh–Taylor不稳定性的离散Boltzmann模拟. 物理学报, 67, 080501 (2018)


https://blog.sciencenet.cn/blog-115136-1199145.html
上一篇:Frontiers of Physics期刊参与2019物理学会秋季会议中国物理学期刊专场报告会
下一篇:【FOP Outstanding Paper】《暗物质及相关宇宙学》专著即将面世