博文
微分和积分的关系
||
学过高等数学的人,都知道一个说法:微分和积分互为逆运算。准确地讲,这句话说的是求导与不定积分的关系。用数学语言严格表达,就是:
命题:(i) 设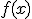 可积,则函数
可积,则函数 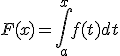 可微且
可微且 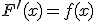 ;
;
(ii) 若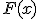 可微,则
可微,则 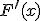 可积且
可积且 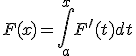 (允许差一常数)。
(允许差一常数)。
这个命题并不是无条件成立的。首先,函数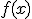 可积时
可积时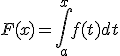 不一定可微,见下边的例1。另一方面,当
不一定可微,见下边的例1。另一方面,当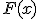 可微时,
可微时,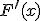 也不一定可积,见下边的例2。
也不一定可积,见下边的例2。
例1. 在[-1, 1]上定义函数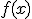 如下:
如下:
例2. 在[-1, 1]上定义函数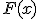 如下:
如下:
我们知道,数学中有很多种积分。前边提到的积分,是指Riemann积分。在Riemann积分范围内,微分与积分的关系只能在一定条件下是互为逆运算。
Lebesgue积分出现之后,可积函数的范围扩大了。还有一个观念性的变化,就是不在乎零测度集,零测度集合上不成立的事可以忽略不计。 因此,例1中的 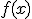 是可微函数。进一步可以证明,在几乎处处意义下,命题的(i)是对的。但(ii)还是不成立,因为例2中的
是可微函数。进一步可以证明,在几乎处处意义下,命题的(i)是对的。但(ii)还是不成立,因为例2中的 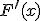 在Lebesgue意义下也不可积。
在Lebesgue意义下也不可积。
问题的最终解决是在非绝对型积分出现之后。非绝对型积分以Henstock-Kurzweil积分为代表,另外的等价形式有Perron积分、 Denjoy积分等。在这类积分中,前边的命题在几乎处处意义下无条件成立。
Henstock-Kurzweil积分产生于上世纪五十年代。有意思的是, Denjoy积分和Perron积分分别出现于1912、1914年,早于Lebesgue积分,但却没有Lebesgue积分知名(有果必有因,原因另文分析)。
(想试试公式编辑器,发现还是有点问题,例1和例2中的函数表达式写不出来,只能插入图片。)
https://blog.sciencenet.cn/blog-112841-436491.html
上一篇:唐诗英译中的又一个“three miles”
下一篇:石三和聂二
全部作者的精选博文
- • 听老外讲汉语
- • 学数学,真的可以成为一种乐趣
全部作者的其他最新博文
- • [转载]杨振宁先生的数学贡献
- • 三星堆vs金字塔
- • 年过完了
- • 闲说教师节(旧文新发)
- • 秋游
- • 此词一出,余词尽废