我们在绪论中提到渐近方法的核心思想和精髓是：通过合理的逐级近似，把一个非常困难、无法直接解决的问题，转化为一系列相对简单、可直接求解的问题。把这一系列相对简单问题都依次解决了，原来的困难问题也算是近似解决了。换成正规一点的表述，即我们无法理解一个复杂的函数表达，但可以把它表示为一系列常见的简单函数组合的形式，而且往往取几项就足够精确了。这一些列简单函数怎么取呢？这就是本章要讲的渐近级数概念。

        有人看到这里会起以前学过的“收敛”级数的概念。我们将看到，“渐近”与“收敛”不是同一个概念，渐近级数一般是发散的。发散级数有意义吗？也能用吗？你我有这样的疑问，其实历史上不少数学大家一开始也有此疑问，并且争议不休。最终结论是，很多情况下，发散的渐近级数很有用，甚至比收敛级数更有用。

        不相信吗？这里就举一个例子。贝塞尔（Bessel，Pierre Etienne Bezier，1910-1999）函数是一类特殊函数，又称柱谐函数或圆柱函数，它一般在分离变量法求解柱坐标下的偏微分方程，如热传导方程、振动方程时遇到。后续课程中，我们会多次与它打交道。贝塞尔函数有好几类不同的形式，互相之间又某种关联，若不加特别说明，一般指第一类贝塞尔函数，它是二阶常微分方程
$$ x^{2} \frac{\textrm{d}^{2} y}{\textrm{d} x^{2}}+x \frac{\textrm{d} y}{\textrm{d} x}+\left(x^{2}-\alpha^{2}\right) y=0 $$
的一个解（$\alpha$等于几就是几阶贝塞尔函数），另一个解是第二类贝塞尔函数（又称诺依曼函数，Neumann function）。此外还有第三类贝塞尔函数（又称汉克尔函数，Hankel function），修正贝塞尔函数、球贝塞尔函数等。一般本科数理方程课上会介绍贝塞尔函数，大家还记得它的函数图像吗？前三阶被贝塞尔函数如图1所示。

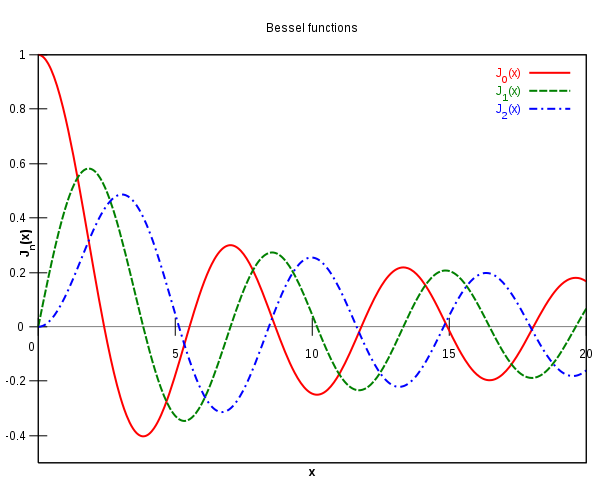
图1 Bessel函数图像（图片来自网络）

       为了计算贝塞尔函数在特定，需要把它用初等函数把它表示出来。对于零阶贝塞尔函数$J_0(x)$，我们可以把它表示为一个\textbf{收敛的幂级数}形式，
\begin{equation}\label{eq:J0-conv}J_{0}(x) =\sum_{n=0}^{\infty}(-1)^{n} \frac{x^{2 n}}{2^{2 n}(n !)^{2}} =1-\frac{1}{4} x^{2}+\frac{1}{64} x^{4}-\frac{1}{2304} x^{6}+\frac{1}{147456} x^{8}-\cdots\end{equation}
       它的收敛半径是无穷大，也就是对任意$x$，它都是收敛的。但是，当$x$较大时，这个交错级数收敛非常慢。当$x=4$时，为了精确到3位有效数字，需要计算8项，得到$J_0(4)=-0.397$。

      我们再来看$J_0(x)$的一个渐近级数表示
\begin{equation}\label{eq:J0-asmp}\begin{aligned}J_{0}(x) & {\sim\left(\frac{2}{\pi x}\right)^{\frac{1}{2}}\left[\left(1-\frac{(3!!)^{2}}{2 !(8 x)^{2}}+\frac{(7 ! !)^{2}}{4 !(8 x)^{4}}-\cdots\right) \cos \left(x-\frac{1}{4} \pi\right)\right.}\\& {\left. +\left(\frac{1}{8 x}-\frac{(5!!)^{2}}{3 !(8 x)^{3}}+\frac{(9 ! !)^{2}}{5 !(8 x)^{5}}-\cdots\right) \sin \left(x-\frac{1}{4} \pi\right)\right]}\end{aligned}\end{equation}
由于分子上有双阶乘的平方，这个级数是快速发散的，但我们只需求1项，就能得到3位有效数字的精度。确实很神奇吧？接下来就让我们好好了解一下发散但好用的渐近级数吧！

历史背景

        级数表示很早就被数学家和工程师们使用，到18世纪初，开始有数学家对收敛与发散的概念进行争论，但是对怎么定义发散级数的和却没有定论。大数学家欧拉等就擅长、且经常不加检验地用到发散级数，他还提出“级数的值就是级数由之而来的代数表达式的值”，如果一个无穷级数是由一个有限表达式展开得到的，那么就可以把二者看作完全等价，而不用管级数到底是不是收敛。由此，我们就可以得到一些奇怪的表达，例如：

$$ 1-1+1-1+1-1+\cdots =\frac{1}{2} $$  
虽然还不理解这些表达的含义，但当时已有不少人对这些奇怪的级数着迷。

        绪论中我们说过，到了19世纪初，数学开始严密化。柯西给出了（收敛）级数的和的严格定义，经典表述为：级数和为级数部分序列和的极限。按照这个定义，上面两个级数和的表示就是错误和荒谬的。从此以后，发散级数基本被排除在数学之外了，这似乎成了一个禁令，很多数学家都不敢使用它。据说，拉普拉斯听完柯西关于级数收敛性的报告，就赶紧回家隐居起来去检查自己《天体力学》书中的每个级数是否收敛。年轻的挪威数学家阿贝尔（Niels Henrik Abel，1802-1829）是柯西的追随者，他曾经说：   

Divergent series are the invention of the devil, and it is shameful to base on them any demonstrations whatsoever. By using them, one may draw any conclusion he pleases and that is why these series have produced so many fallacies and so many paradoxes.}    
    发散级数是魔鬼的发明。把不管什么样的任何证明建立在发散级数的基础之上都是一种耻辱。利用发散级数人们想要什么结论就可以得到什么结论，而这也是发散级数已经产生了如此多的谬论和悖论的原因。

      但后人还发现阿贝尔也说过这样的话：

    That most of the things are correct in spite of that is extraordinarily surprising. I am trying to find a reason for this; it is an exceedingly interesting question.   
    尽管非常奇怪，它（发散级数）很多时候都是正确的。我正在设法找出原因，这真是太有意思了。

       可见，人们还是不能无视发散级数的神秘魅力。事实上，柯西本人有时也会忍不住用一下发散级数，还写了一篇文章《论发散级数的合理运用》。也有其他数学家不顾“禁令”，继续使用发散级数，还试图弄清它到底有何意义。还记得绪论中提到的发明运算微积法的赫维赛德（Heaviside ）吧？他甚至说“就是因为级数是发散的，我们才能用它来做些事情（The series is divergent; therefore, we may be able to do something with it）。”

        最终，到19世纪末，庞加莱（Poincare）和斯蒂尔杰斯（Thomas Joannes Stieltjes，1856-1894）几乎同时独立地提出了渐近级数的概念。我们不用管发散级数无穷多项怎么求和，而是利用它的有限项来逼近目标函数的极限行为。还有其他数学家给出了不同于传统定义的发散级数求和的一些新定义，不同定义求和结果可能不同，但都有某种特殊意义和应用。发散级数终于被恢复名誉，并在很多领域得到应用。发散级数从被禁止到再被接纳甚至推崇的过程，被庞加莱成为“我们科学的一个奇怪的变迁”，这一变迁体现了应用数学家不拘泥旧框框、大胆接受新想法而推陈出新的实用主义和勇于探索精神。

       发散级数的一个重要用途就是计算积分和解微分方程，这也是本课程的主要内容。我们可以先列出三个典型例子，在后续章节再加以证明。

      1，斯特林（James Stirling，1692-1770）公式。在统计物理中常常用到的自然数阶乘近似公式：  
$$m!=\sqrt{2\pi m}m^m \textrm{e}^{-m}$$    
其实是下面渐近公式的头几项，    
$$ \ln m ! \sim\left(m+\frac{1}{2}\right) \ln m-m+\frac{1}{2} \ln 2 \pi+\sum_{n=1}^{\infty} \frac{\varphi_{2 n}(0)}{(2 n-1) 2 n \cdot m^{2 n-1}} $$    
其中$ {\varphi_{2 n}(0)} $是可以递推计算的Bernoulli数。

2，余误差函数的渐近展开。Laplace在其《概率的解析理论中》给出，对于很大的$ T $，  
$$ \textrm{erfc}(T) =\int_{T}^{\infty} e^{-t^{2}} d t  \sim \frac{e^{-T^{2}}}{2 T}\left(1-\frac{1}{2 T^{2}}+\frac{1 \cdot 3}{\left(2 T^{2}\right)^{2}}-\frac{1 \cdot 3 \cdot 5}{\left(2 T^{2}\right)^{3}}+\cdots\right) $$

3，Laplace积分。同样在《概率的解析理论中》，Laplace给出  
$$ I=\int_{a}^{b} g(t) e^{x h(t)} \textrm{d} t \sim g(a) e^{x h(a)} \sqrt{\frac{-\pi}{2 x h^{\prime \prime}(a)}} $$    
其中，$x\to \infty$，假定函数$h(t)$在区间$[a,b]$的$a$点取最大值，且$h'(a)=0$。

渐近级数的定义

量阶、大O与小o

       请看图2，一般人会觉得“不平衡”、“不协调”，甚至脑子里会闪现一句话：这两个人不是一个“量级”的。如果是看两个相扑运动员对战，或者两个小孩摔跤打架，我们就没有觉得异样，但是为何看到一个运动员对阵一个小孩子，就觉得非同寻常呢？这反映了人们脑子中天然就有“量级”的概念。

图2 日常生活中的“量级”：相扑运动员与小孩（图片来自网络）

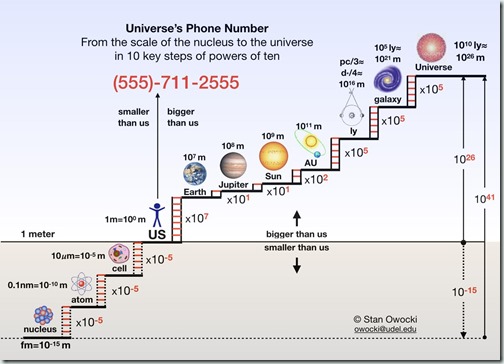
图3 宇宙中各类现象的特征尺度（图片来自网络）

        自然现象和事物天然有量级的差别，人类也已发展出一系列对应的单位制，如图3所示。同样是长度单位，在原子分子研究领域，一般用纳米或埃米，在日常生活中我们常用到厘米或米，而天文学家则常用天文单位（地日平均距离）或者光年。对于时间单位也类似，有纳秒、秒、分、小时、年等单位。我们从不说某人身高多少纳米或零点零零……几光年，也不说每节课要上多少纳秒或零点零零……几年。为什么呢？我们天然就知道，衡量某件事物或过程，就要用与它特征尺度差不多的单位，也就是说同一个量级的，才好描述。另外，当涉及不同量级的比较时，人们也会自然地做取舍，有一句俗语“捡了芝麻，丢了西瓜”用来讽刺那些不懂量级“轻重”的人，路边小摊上卖菜卖水果的小贩在顾客结帐时常把零钱抹掉，你买衣服时能把价钱从350砍到300，算是正常的，但是如果想砍到30，卖家就要生气了，如果卖家不生气还爽快答应了，那说明对方想骗你。另外，从生活常识我们也知道，量级还暗含着“比较”、“相对”的意义，只有在两相比较时才有意义。例如，买一个2000元的手机，卖家可能会送一个几十元的耳机，因为相对来说，几十元是小量，2000元是大量；但是，在买几十万的汽车，甚至几百万的房子时，2000元就成可忽略的小量了。这些都是人们对“量级”朴素的认识。

        接下来我们就从数学上看看它的定义和运算规则。

定义1：设$\Phi(x)$，$\phi(x)$是定义在$\Omega$上的两个函数。如果存在某个常数$A$，使得对$\Omega$某个内点$x_0$的邻域$U$内的所有$x$，满足    
\begin{equation} \abs{\Phi(x)}\le A \abs{\phi(x)} \qquad \textrm{or,} \qquad \lim\limits_{x\to x_0}\abs{\dfrac{\Phi(x)}{\phi(x)}}=A \end{equation}    
我们就称函数$\Phi(x)$至多与$\phi(x)$同阶，或同量级，记为    
\begin{equation}\label{eq:big-O} \Phi(x)=O\left(\phi(x)\right), \qquad x\to x_0 \end{equation}

定义2：设$\Phi(x)$，$\phi(x)$是定义在$\Omega$上的两个函数。对于任一$\varepsilon>0$，$\Omega$某个内点$x_0$总有一个邻域$U_\varepsilon$存在，使得所有$\varepsilon \in U_\varepsilon$满足    
\begin{equation}  \abs{\Phi(x)}\le \varepsilon \abs{\phi(x)} \qquad \textrm{or,} \qquad \lim\limits_{x\to x_0}\abs{\dfrac{\Phi(x)}{\phi(x)}}=0    \end{equation}    
我们就称在$x\to x_0$时，函数$\Phi(x)$是$\phi(x)$的高阶小量，记为    
\begin{equation}\label{eq:little-o}  \Phi(x)=o\left(\phi(x)\right), \qquad x\to x_0 \end{equation}

容易证明，量级表示有下述性质：  
\begin{equation}    \begin{aligned}   & O\left[O(\phi)\right]=O(\phi)\\    & O(\phi)\cdot O(\psi)=O(\phi \cdot \psi) \\    & O(\phi)+O(\phi)=O(\phi)    \end{aligned}    \end{equation}

     注意，当我们用 big $O$或 little $o$符号时，是不必写常系数的。另外，在本课程推导中，若非特别说明，“$x\to 0$”一般默认指 “$ x\searrow 0^+ $”。当然，对于$x$为负值的情况，也可相应推导。例如，  
\begin{equation}  \begin{aligned}    & \sin 2 x=O(x)\\  & 1-\cos x=O\left(x^{2}\right)=o(x)\\    & \operatorname{ctg} x=O\left(\frac{1}{x}\right)\\  
& \sec ^{-1}(1+x)=O\left(x^{\frac{1}{2}}\right)=o(1)    \end{aligned}    \qquad x\to 0    \end{equation}    
     为了展示复杂函数量级的求法，这里简单推导一下最后一个式子，    
\begin{gather*}  \sec ^{-1}(1+x)=y, \quad 1+x=\sec y= \dfrac{1}{\cos y}= \dfrac{1}{1- y^2/2+O(y^4)}= 1+y^2/2+O(y^4),\\    \therefore \quad x= O(y^2),\quad y=O(x^{\frac{1}{2}}), \quad x\to 0   \end{gather*}

      在上述定义中，原则上对函数$\phi(x)$并没什么要求，但我们一般总是取幂函数、对数函数、指数函数等这类初等函数，以方便我们形象、直观地了解某一函数量阶的大小。这里之所以要补充对数函数和指数函数，是因为有时幂函数还不足以描述某些函数的量阶，如  
\begin{equation}  \begin{aligned}    & \sech^{-1} x=O(\ln \frac{1}{x})\\  & \cosh \frac{1}{x}=O\left(\mathrm{e}^{1/x}\right)\\    \end{aligned}    \qquad x\to 0  \end{equation}    
        我们再推导一下第一个式子，   
\begin{gather*}  \sech^{-1} x=y, \quad x=\sech y=\dfrac{1}{\cosh y} =\dfrac{2}{\mathrm{e}^y+\mathrm{e}^{-y}}, \quad \mathrm{e}^{2y}-\dfrac{2}{x}\mathrm{e}^y+1=0\\    \therefore \quad \mathrm{e}^y=\dfrac{2/x\pm\sqrt{4/x^2-4}}{2}=\dfrac{1}{x}\pm \sqrt{\dfrac{1}{x^2}-1}=\dfrac{2}{x}+o(\dfrac{1}{x}) \quad \textrm{or} \quad \dfrac{x}{2}+o(x), \\ 
\therefore \qquad y=O(\ln x) ~ \textrm{or} ~O\left(\ln \dfrac{1}{x}\right) \quad x\to 0    \end{gather*}    
其实，从$\quad x=\frac{2}{\mathrm{e}^y+\mathrm{e}^{-y}}\to 0$已经可以推测，要么$x=O(\mathrm{e}^y)$，要么$x=O(\mathrm{e}^{-y})$。

      请注意，对数函数要比任意次幂函数变化得更慢，指数函数要比任意次幂函数变化得要快，所以  
\begin{equation}  \begin{aligned}   & \textrm{For~any~large }~m,~\exp\left(-\dfrac{1}{x}\right)=o\left(x^m\right)\\   & \textrm{For~any~small }~n,~x^n=o\left(-\dfrac{1}{\ln x}\right)\\   \end{aligned} \qquad x\to 0  \end{equation}    
反过来，当 $~\xi\to +\infty~$时，    
\begin{equation}  \begin{aligned} & \textrm{For~any~large }~m,~\xi^m=o\left(\mathrm{e}^\xi \right)\\    & \textrm{For~any~small }~n,~\ln \xi=o\left(\xi ^n\right)\\    \end{aligned}    \qquad \xi\to +\infty    \end{equation}

所以，在渐近幂级数展开中，$\exp\left(-\dfrac{1}{x}\right)$是超越小量（exponentially small term，EST），在渐近对数级数展开中，$x^n$是超越小量，均可直接略去。  

渐近级数

       在以上量级表示中，只保留了最主要的项，且忽略掉了常系数，这只能对某函数的变化特征形成最初步的认识，类似于“雾里看花，水中望月”。人们对事物的认识，总是有一个逐渐加深、“精益求精”的过程。好比一个近视但没带眼镜的人，看另一个人由远及近，他先朦朦胧胧看到有一个人，近一点能看清穿衣打扮、年龄性别，再近一点能看清眉目嘴脸，认得是张三李四了，最后拿个放大镜贴上去看，就能看到脸上的雀斑汗毛了。数学近似同样如此，有一个由粗到精的过程。接下来，按照准确程度的次序，阐述六种描写极限过程的方式，对渐近级数的引入和定义做一个介绍。   

    1，定性上说，当$~x\to 0~$时，某函数 $f(x)$是否存在极限。

    2，如果有极限，再分三种情况：$0$、有限值、$\infty$。

    3，准确给出有限的极限值：$\lim\limits_{x\to 0}f(x)=C$。

    以上三种方式，只告诉我们取极限的最终结果，没有描述函数以何种方式和速率趋于极限，可进一步改进。

    4，为了用量阶符号表示趋于极限的速率，引入标准函数$\delta (x)$（一般是我们熟悉的初等函数），表示出
\[f(x)=O\left[\delta(x)\right] \qquad \textrm{or} \qquad  f(x)=o \left[\delta(x)\right] \]

    5，比上述表示更准确化，如果  
\begin{equation}    f(x)=C \delta (x)+o\left[\delta(x)\right]    \end{equation}    
则$f(x)$的渐近表示为    
\begin{equation}  f(x)\sim C\delta (x)    \end{equation}    
    请从以上两式，\textbf{体会等号“$ =$”与等价符号“$ \sim $”用法的区别}。渐近表示是原先函数的近似值，其误差是高阶小量。

两个例子：$\sin 2x \sim 2x \qquad \sech^{-1} \sim \ln \frac{2}{x}$

    6，以上我们算是抓住了主要矛盾，接下来还要进一步兼顾次要矛盾，即分析$C \delta (x)$与$f(x)$的差异——余项趋于零的方式和速率。这样依次类推，无限进行下去，我们就得到函数性态更加精确化的描述，即渐近级数或渐近展开。

    定义：对于标准函数系$\{\delta_n (x) \}$，满足$\delta_{n+1} (x)=o[\{\delta_n (x) \}]$，若函数$f(x)$可表示为  
\begin{equation}    f(x)=\sum_{n=1}^{N} C_{n} \delta_{n}(x)+o\left[\delta_{N}(x)\right]    \end{equation}    
那么，我们称$\sum_{n=1}^{N}C_n \delta_{n}(x)$为函数$f(x)$的$N$项渐近级数或渐近展开，记为    
\begin{equation}    f(x) \sim C_{1} \delta_{1}(x)+C_{2} \delta_{2}(x)+\cdots+C_{N} \delta_{N}(x)    \end{equation}    
    如果对于任意大小的$N$， 上式都成立，那么我们就得到了无穷渐近展开    
\begin{equation}    f(x)\sim \sum_{n=1}^{\infty}C_n \delta_{n}(x)    \end{equation}

    根据渐近级数的定义，我们可以知道，对选定的渐近序列$\{\delta_n (x) \}$，渐近级数的系数是唯一确定的。但如果选不同的渐近序列，如$x^n$和$\sin ^n x$，同一个函数可以有不同的渐近展开。反过来说，不同的函数，只要相差超越无穷小项，也可以有相同的渐近展开。如果渐近级数的标准函数序列是幂函数，我们就称它为渐近幂级数。

仍然举之前的例子：  
\begin{equation}    \begin{aligned}    & \sin 2 x \sim 2 x-\frac{4}{3} x^{3}+\frac{4}{15} x^{5}-\cdots\\    & \sech^{-1} x \sim \ln \frac{2}{x}+\frac{1}{4} x^{2}+\frac{3}{32} x^{4}+\cdots    \end{aligned}    \qquad x\to 0    \end{equation}    

渐近与收敛

        刚学渐近时，很容易把渐近与收敛这两个概念混淆起来。学了渐近级数的定义后，现在可以对比一下渐近与收敛的区别了。

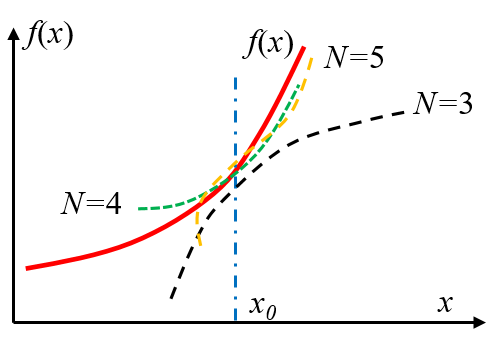
图4 收敛和渐近对比示意图

     1，收敛指在$x$固定，函数项级数$\sum_{n=1}^{\infty}C_n \delta_{n}(x)$的项数$N$趋于无穷时，级数的部分和有极限$f(x)$，即    
$$\lim\limits_{N\to \infty}\sum_{n=1}^{N}C_n \delta_{n}(x)\to f(x).$$    
所以，对于\textbf{收敛级数，项数取得越多，结果就越精确}，如图4左所示。而渐近指的是当\textbf{项数$N$固定，变量$x\to x_0$时，结果越精确}，即    
$$\lim\limits_{x\to x_0}\sum_{n=1}^{N}C_n \delta_{n}(x)\sim f(x_0),$$    
如图4右所示。对于固定的$x$，精度是由一定限制的，单纯增加项数往往无济于事。

    2，收敛的级数是指函数与级数部分和相差的\textbf{绝对误差}小，即$$\lim\limits_{N\to \infty}\sum_{n=N+1}^{\infty}C_n \delta_{n}(x)\to 0.$$  
渐近级数是指函数与有限渐近级数和的差所表示的余项的\textbf{相对误差}很小，即余项   
$$R_N=\lim\limits_{x\to x_0} \sum_{n=N+1}^{\infty}C_n \delta_{n}(x)\ll C_N \delta_{N}(x).$$    
从实用意义上讲，我们只要相对误差小就可以了，这就可以保证有一定的有效数字。   

    3，收敛级数与发散渐近的各项大小与性态会有本质的区别。收敛级数的项，当 $ n $ 充分大以后，总要趋于零的，即  
$$\lim\limits_{N\to \infty}C_N \delta_{N}(x) \to 0.$$    
发散的渐近级数，往往后面的项会逐步增大。这往往使人迷惑不解，其实当$x\to x_0$时，后面的项最终总会小于前面项，即    
$$\lim\limits_{x\to x_0} \dfrac{C_{N+1} \delta_{N+1}(x) }{C_N \delta_{N}(x) }\to 0. $$

实际计算中，渐近级数的余项是最后一项的高阶小量（但并不等于余下级数的部分和），优于缓慢收敛的级数求和。

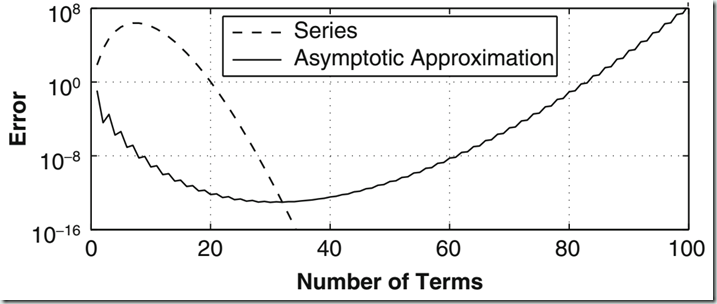
图5 Bessel函数$ J_0(15) $计算结果相对误差随项数变化（图片来自网络）

        既然渐近级数并非项数取得愈多愈好，就有一个最佳截断(optimal truncation)，图5显示了我们用最上面的两个式子计算$ J_0(15) $时，相对误差随项数的变化，可见渐近级数取某一项数时，相对误差最小。我们知道，$ N $ 项渐近级数的余项为 $ O[\delta_{N+1}(X)] $， 即    
\begin{equation*}   f(x)=\sum_{n=1}^{N} C_{n} \delta_{n}(x)+O\left[\delta_{N+1}(x)\right]    \end{equation*}    
所以，如果第 $ N+1 $ 项是最小的项，从 $ N+2 $项起开始增大了，那么我们取 $ N $ 项的渐
近级数的余项是最小的，即该渐近级数只有取 $ N  $项才是最准确的。用相对误差来表示，就是    
\begin{equation*}  \abs{\dfrac{C_{N+1}\delta_{N+1}(x)}{f(x)}}<\abs{\dfrac{C_{N}\delta_{N}(x)}{f(x)}}, \qquad \abs{\dfrac{C_{N+1}\delta_{N+1}(x)}{f(x)}}<\abs{\dfrac{C_{N+2}\delta_{N+2}(x)}{f(x)}}    \end{equation*}    
我们称    
\begin{equation*}    f(x)\sim \sum_{n=1}^{N} C_{n} \delta_{n}(x)    \end{equation*}    
    为原渐近级数的最佳截断。显然，最佳截断的项数 $ N $ 依赖于 $ x  $，即 $ N = N(x) $。

    我们以余误差函数的最佳截断为例来说明渐近级数计算的方法和过程。我们以后会知道余误差函数的渐近展开为  
\begin{equation}    \operatorname{erfc}(T) \sim \dfrac{e^{-T^{2}}}{2 T}\left[1+\sum_{n=2}^{\infty}(-1)^{n-1} \dfrac{(2 n-3) ! !}{\left(2 T^{2}\right)^{n-1}}\right]    \end{equation}    
为了求最佳截断，我们得到    
\begin{equation}    \dfrac{a_{n+1}}{a_{n}}=\frac{2 n-1}{2 T^{2}} \geq 1, \qquad \Rightarrow \qquad n\ge T^2+\dfrac{1}{2}    \end{equation}    
即级数中绝对值最小的项为$\left[T^2+\dfrac{1}{2}\right]$或$\left[T^2+\dfrac{1}{2}\right]+1$处，最佳截断取在    
\begin{equation}    N=\left[T^2+\dfrac{1}{2}\right]-1  \end{equation}    
处。若$T=2$，则$N=4$；若$T=3$，则$N=9$。    

渐近级数的性质

    一些基本的运算性质，

    1，和差运算：  
\begin{equation}      \left\{    \begin{array}{lr}    f(x)\sim \sum_{n=1}^{\infty}f_n \delta_{n}(x) &  \\    g(x)\sim \sum_{n=1}^{\infty}g_n \delta_{n}(x) &  \end{array}   
\right.    \qquad \Rightarrow  \qquad af(x) \pm bg(x)\sim \sum_{n=1}^{\infty}(af_n \pm bg_n) \delta_{n}(x)     \end{equation}

    2，幂级数序列乘除运算：  
\begin{equation}    \begin{array}{lr}    f(x)\sim \sum_{n=1}^{\infty}\dfrac{f_n}{x^n}, \qquad g(x)\sim \sum_{n=1}^{\infty}\dfrac{g_n}{x^n}, \qquad x\to \infty   &\\      f(x) \cdot g(x)= \sum_{n=1}^{\infty}\dfrac{c_n}{x^n}, \qquad c_n=\sum_{j=0}^{n}f_j g_{n-j} &\\      g_0\ne0,\quad \dfrac{f(x)}{g(x)}\sim \sum_{n=0}^{\infty}\dfrac{d_n}{x^n}, \qquad f_m=\sum_{j=0}^{m}d_j g_{m-j} & 
\end{array}    \end{equation}

    3，幂级数序列积分运算（$f(x)$如上，在$x>a>0$时连续）：  
\begin{equation}   F(x)=\int_{x}^{\infty} \left(f(t)-f_0-\dfrac{f_1}{t}\right)\sim \sum_{n=1}^{\infty}\dfrac{f_{n+1}}{n x^n}    \end{equation}

    4，幂级数序列微分运算  
\begin{equation}    f'(x)=-\sum_{n=2}^{\infty}\dfrac{(n-1)f_{n-1}}{ x^n}    \end{equation}

    渐近级数的定义和微分运算可推广到复平面，有两个定理，略。  

隐函数的渐近分析

    反函数定理证明，略。本课程主要学习微分和积分方程的渐近求解，对于隐函数分析，此处仅演示两个直接用渐近级数求解的例子，相关定理和推理不再证明，感兴趣者请自学。

    1，求方程 $x=\mathrm{ctan}x$在$x\to +\infty$时的根。

分别画出$f(x)=x$与$f(x)=\mathrm{ctan}x$函数的图像，如图6所示，可见在$x$很大时，两曲线交点横坐标仅比$n\pi$大一点，因此，可以先假设$x_n=n\pi+\delta_{1}$，其中$ \delta_{1}\ll 1 $，则  
\begin{gather*}    n\pi+\delta_{1}=\mathrm{ctan} n\pi+\delta_{1})=\mathrm{ctan}(\delta_{1})=\dfrac{1}{\delta_{1}}-\dfrac{\delta_{1}}{3}+O\left(\delta_{1}^3\right) \\    \therefore \quad  \delta_{1}\sim \dfrac{1}{n\pi}  \qquad x_n\sim n\pi+\dfrac{1}{n\pi} \quad n\to \infty    \end{gather*}    
 可进一步令$x_n=n\pi+\dfrac{1}{n\pi}+ \delta_{2}$，进一步求下去，一般求一两步修正就足够精确了。    

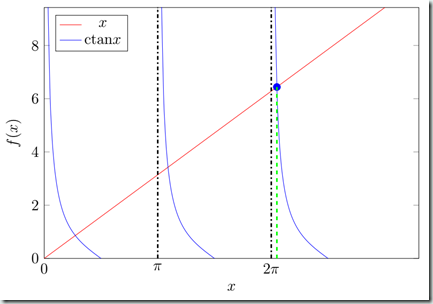
图6 函数$f(x)=x$与$f(x)=\mathrm{ctan}x$

    2，求方程 $x\mathrm{e}^x=t$在$t\to +\infty$时的根。    
\begin{gather*}    x+\ln x=\ln t,     \qquad \because ~ \ln x =o(x), \qquad \therefore x=\ln t + x_1, \quad x_1=o(\ln t)\\    x_1+\ln \left(\ln t+x_1\right) =0, \quad x_1+\ln \left[\ln t \left(1+\dfrac{x_1}{\ln t }\right)\right]= x_1+\ln \ln t + \dfrac{x_1}{\ln t }+O\left[\left(\dfrac{x_1}{\ln t }\right)^2\right],\\ x_1= -\dfrac{\ln \ln t}{1+\dfrac{1}{\ln t }} +\cdots=-\ln \ln t+ \dfrac{\ln \ln t}{\ln t} +o\left[\dfrac{\ln \ln t}{\ln t}\right], \\    \therefore  \quad x \sim \ln t- \ln \ln t + \dfrac{\ln \ln t}{\ln t} \quad t\to \infty    \end{gather*}    
依次类推，可一直求下去。   

    2020年2月25日完成初稿。